Mathematica Helps Discover the Largest Known Prime Number
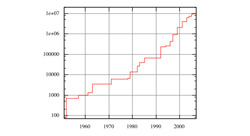
In June 1999 an international group of mathematicians, computer scientists, and hobbyists, who had joined under the banner of the Great Internet Mersenne Prime Search (GIMPS), discovered that 26972593-1 is prime. The number is currently the largest known prime. The discoverers are officially listed as N. Hajratwala, G. Woltman, and S. Kurowski, the first person being the volunteer whose machine actually found the prime and the latter persons being the software/network architects. This prime is 2,098,960 decimal digits long and therefore qualifies for a $50,000 prize from the Electronic Frontier Foundation. One interesting sidelight is that in the early 1990s Mathematica played an important part in making the discovery possible.
First some historical perspective: prime numbers of the form 2q-1 are named "Mersenne primes" after the French monk Marin Mersenne (1588-1648), who discussed them in correspondence with the great Fermat. Mersenne primes have long played an important role in number theory—for example, in the theory of so-called perfect numbers and in cryptography, where certain algebraic fields enjoy efficient, Mersenne-based arithmetic. Though Mersenne primes have been studied for centuries, many fundamental questions remain, including whether an infinite number of them exist.
The only way to determine whether a very large number is really prime is to run a so-called primality test, which in the case of Mersenne primes can be an efficient manifestation called the Lucas-Lehmer test. The Lucas-Lehmer test involves the squaring of giant numbers—numbers with thousands or millions of digits.
For such arithmetic, the underlying algorithm—an "irrational base discrete weighted transform" (IBDWT)—was developed in the early 1990s by R. Crandall at Reed College and NeXT, Inc., using Mathematica as a prototyping environment. It was this algorithm that Woltman cast in the mid-1990s as an assembler variant, thus completing the prototyping/development cycle for which Mathematica is ideal.
The idea of the IBDWT is to expand giant numbers in an irrational base. One then applies a discrete weighted transform—a variant of the classical FFT—to multiply or square numbers in this base with unprecedented speed. As Crandall puts it: "Mathematica is an ideal environment for the requisite mixing of symbolics and numerics and the kind of interactive exploration that leads to such a new, nonstandard algorithm."
A prime-number wall poster, showing all decimal digits (more than two million of them) for the record prime number is available from Perfectly Scientific, Inc.
Get started with Wolfram technologies, or work with us to apply computational expertise to your projects.
Questions? Comments? Get in touch: 1-800-WOLFRAM, or email us »