Solve an Initial Value Problem for the Wave Equation

Specify the wave equation with unit speed of propagation.

In[1]:=

weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}];

Prescribe initial conditions for the equation.

In[2]:=

ic = {u[x, 0] == E^(-x^2), Derivative[0, 1][u][x, 0] == 1};

Solve the initial value problem.

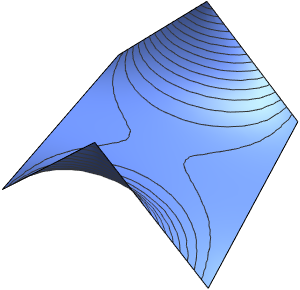
In[3]:=

DSolveValue[{weqn, ic}, u[x, t], {x, t}]

Out[3]=

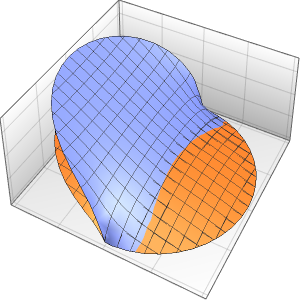
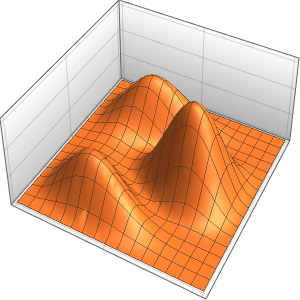
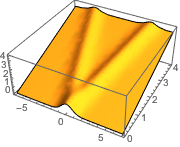
The wave propagates along a pair of characteristic directions.

In[4]:=

DSolveValue[{weqn, ic}, u[x, t], {x, t}]; Plot3D[%, {x, -7, 7}, {t, 0, 4}, Mesh -> None]

Out[4]=

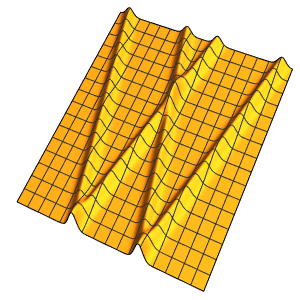
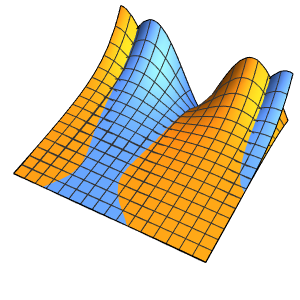
Solve the initial value problem with piecewise data.

In[5]:=

ic = {u[x, 0] == UnitBox[x] + UnitTriangle[x/3], Derivative[0, 1][u][x, 0] == 0};

In[6]:=

DSolveValue[ {weqn, ic}, u[x, t], {x, t}]

Out[6]=

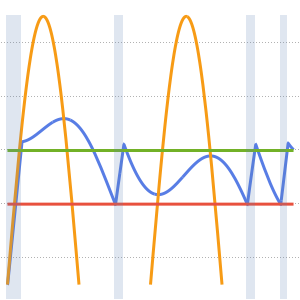
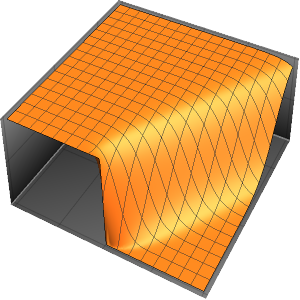
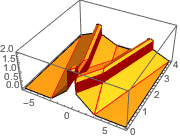
Discontinuities in the initial data are propagated along the characteristic directions.

In[7]:=

DSolveValue[ {weqn, ic}, u[x, t], {x, t}]; Plot3D[%, {x, -7, 7}, {t, 0, 4}, PlotRange -> All, Mesh -> None, ExclusionsStyle -> Red]

Out[7]=

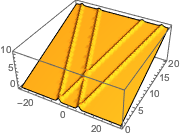
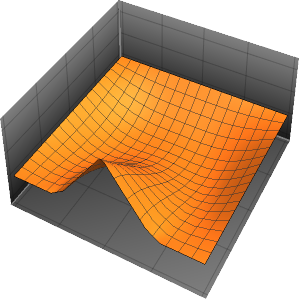
Solve the initial value problem with a sum of exponential functions as initial data.

In[8]:=

ic = {u[x, 0] == E^(-(x - 6)^2) + E^(-(x + 6)^2), Derivative[0, 1][u][x, 0] == 1/2};

In[9]:=

sol = DSolveValue[ {weqn, ic}, u[x, t], {x, t}]

Out[9]=

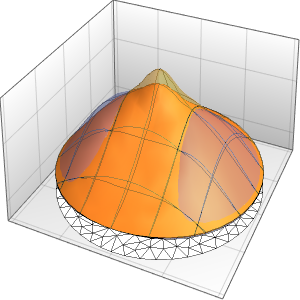
Visualize the solution.

In[10]:=

Plot3D[sol, {x, -30, 30}, {t, 0, 20}, PlotRange -> All, Mesh -> None, PlotPoints -> 30]

Out[10]=