Explore Isoperimetric Quotient of Polyhedra

The ratio of the surface area of a solid to its volume gives a measure of how efficiently its content is enclosed. As is well known, this ratio is minimized for the ball.

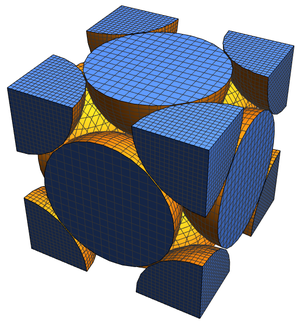
To explore the relationship between surface area and volume for polyhedra, extract the surface area, volume and generalized diameter for non-compound "Polyhedron" entities.

Now form the list of the (suitably scaled) surface area–to–volume ratios for each polyhedron.

Examining the largest and smallest ratios reveals the snub dodecahedron (which well approximates a sphere and so has ratio near 3) and highly stellated spiky echindahedron as the extremal cases.

In fact, by this measure, the conventional soccer ball shape (the truncated icosahedron) ranks only #9 of the tabulated polyhedra in terms of how well it approximates a sphere.

Plotting all the data shows a general trend from smooth solids with ratios around 3 to spiky solids with arbitrarily large ratios.