Vector Analysis & Visualization
In the Wolfram Language, n-dimensional vectors are represented by lists of length n.
Calculate the dot product of two vectors:
| In[1]:= |
| Out[1]= |
Type ESCcrossESC for the cross product symbol:
| In[2]:= |
| Out[2]= |
Calculate a vector’s norm:
| In[1]:= |
| Out[1]= |
Find the projection of a vector onto the x axis:
| In[2]:= |
| Out[2]= |
Find the angle between two vectors:
| In[3]:= |
| Out[3]= |
Calculate the gradient of a vector:
(For the∇ symbol, use ESCgradESC.)
| In[1]:= |
| Out[1]= |
Compute the divergence or curl of a vector field:
| In[2]:= |
| Out[2]= |
The Wolfram Language has 2D and 3D functions suitable for visualizing vector fields:
| In[1]:= |
| Out[1]= | 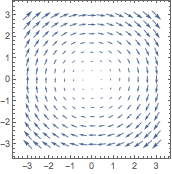 |
| In[2]:= |
| Out[2]= | 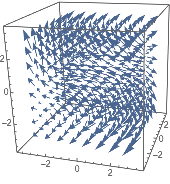 |
Plot a vector field over a slice surface:
| In[3]:= |
| Out[3]= | 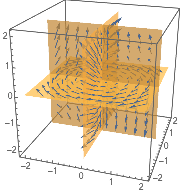 |
QUICK REFERENCE: Vector Analysis »
QUICK REFERENCE: Vector Visualization »
