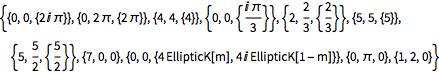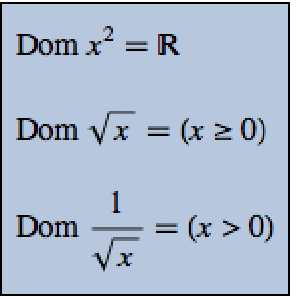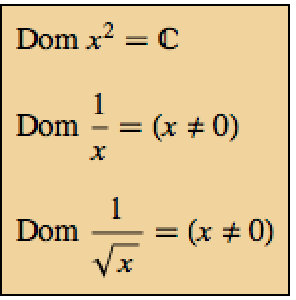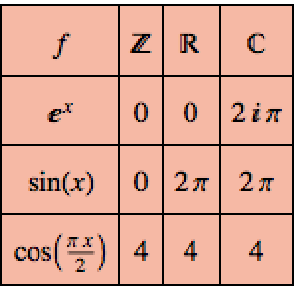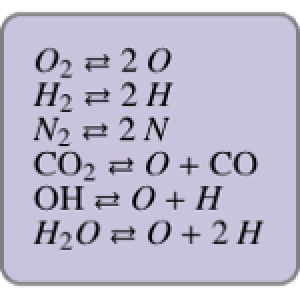Compare Periods over Different Domains
The periodicity properties of a function may differ as it is considered over different domains. The following command compares the period of a function over the integers, reals, and complexes.
Famously, the exponential function has an imaginary period.
| Out[3]= | 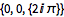 |
Functions can be periodic over the reals only or integers only as well.
| Out[4]= | 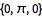 |
| Out[5]= | 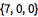 |
show complete Wolfram Language inputhide input
| Out[6]= | 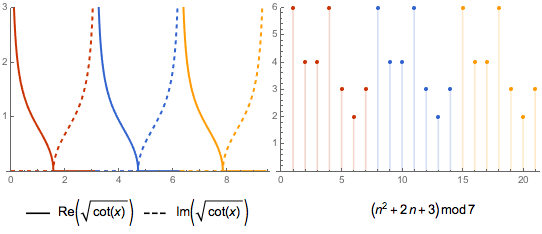 |
On the other hand, power functions involving roots of 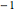 are periodic over all three domains.
are periodic over all three domains.
| Out[7]= | 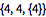 |
| Out[8]= | 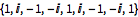 |
It is easy to compare the domains for many different functions.
| Out[10]= | 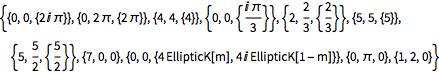 |
Nicely format the results.
show complete Wolfram Language inputhide input
| Out[11]//TraditionalForm= |
| | 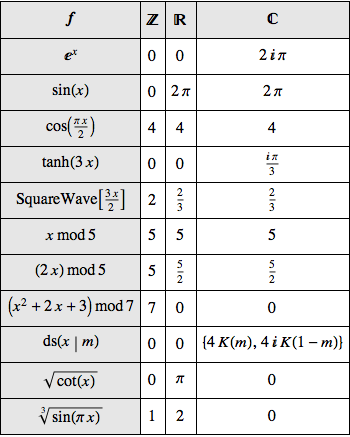 |

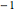 are periodic over all three domains.
are periodic over all three domains.