Quantum Hamiltonian 

In standard quantum mechanics, systems evolve according to the Schrödinger equation 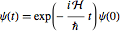, where 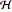is a Hermitian matrix called the Hamiltonian. The following are possible Hamiltonians.

In[1]:=

X \[ScriptCapitalH]1 = {{0, -I}, {I, 0}}; \[ScriptCapitalH]2 = {{1, 0, 1 + I}, {0, 1, 0}, {1 - I, 0, 2}};

In[2]:=

X {HermitianMatrixQ[\[ScriptCapitalH]1], HermitianMatrixQ[\[ScriptCapitalH]2]}

Out[2]=

The following matrices cannot be quantum Hamiltonians because they are not Hermitian.

In[3]:=

X bad1 = {{0, 1}, {-1, 0}}; bad2 = {{1, 0, I}, {0, 1 - I, 2}, {-I, 1 + I, 5}};

In[4]:=

X {HermitianMatrixQ[bad1], HermitianMatrixQ[bad2]}

Out[4]=

The matrix exponential is called the time-evolution operator and is always a unitary matrix (assuming the time 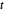and Planck's constant ℏ are real).

In[5]:=

X u1 = MatrixExp[-((I \[ScriptCapitalH]1)/\[HBar]) t]

Out[5]=

In[6]:=

X u2 = MatrixExp[-((I \[ScriptCapitalH]2)/\[HBar]) t]

Out[6]=

In[7]:=

X Function[m, UnitaryMatrixQ[m, SameTest -> (Simplify[#1 == #2, {t, \[HBar]} \[Element] Reals] &)]] /@ {u1, u2}

Out[7]=