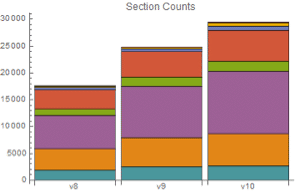
Study the Stochastic Exponential Function 

Define the stochastic exponential of the Wiener process as a transformed Wiener process.

In[1]:=

X \[ScriptCapitalE]w = TransformedProcess[E^(w[t] - (\[Sigma]^2 t)/2), w \[Distributed] WienerProcess[0, \[Sigma]], t];

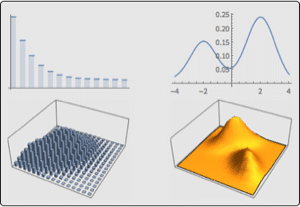
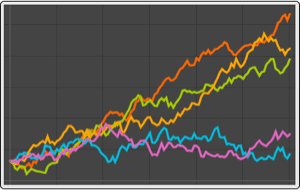
Simulate the process.

In[2]:=

X data = RandomFunction[\[ScriptCapitalE]w /. \[Sigma] -> 1, {0, 10, 0.01}, 4];

In[3]:=

X ListLinePlot[data, PlotRange -> All]

Out[3]=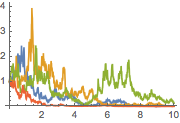

Compute the mean and variance for a time slice of the process.

In[4]:=

X {Mean[\[ScriptCapitalE]w[t]], Variance[\[ScriptCapitalE]w[t]]}

Out[4]=

Compare with the result using the corresponding SDE .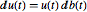

In[5]:=

X \[ScriptCapitalE]sde = ItoProcess[\[DifferentialD]u[t] == u[t] \[DifferentialD]b[t], u[t], {u, 1}, t, b \[Distributed] WienerProcess[0, \[Sigma]]];

In[6]:=

X {Mean[\[ScriptCapitalE]sde[t]], Variance[\[ScriptCapitalE]sde[t]]}

Out[6]=

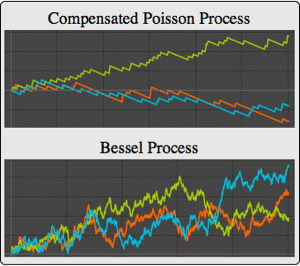
Define the stochastic exponential of the compensated Poisson process as a transformed Poisson process.

In[7]:=

X \[ScriptCapitalE]p = TransformedProcess[2^p[t] Exp[-\[Lambda] t], p \[Distributed] PoissonProcess[\[Lambda]], t];

In[8]:=

X ListLinePlot[ RandomFunction[\[ScriptCapitalE]p /. \[Lambda] -> 1, {0, 10, 0.01}, 4], PlotRange -> All]

Out[8]=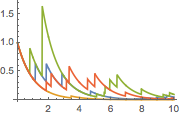

In[9]:=

X {Mean[\[ScriptCapitalE]p[t]], Variance[\[ScriptCapitalE]p[t]]}

Out[9]=