Heart Rate Estimation from Video
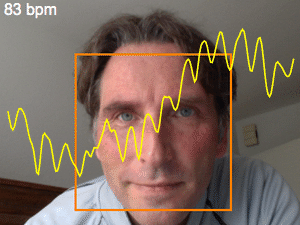
Changes to skin color due to blood flow in the skin can be captured on video and used to find an estimate of heart rate. Although such a change is too small to be seen by the human eye, the signal can be nicely extracted and analyzed from the skin pixels in consecutive frames.
Acquire frames of a video and its acquisition times.
| In[1]:= |  X |
| In[2]:= | X |
Determine the bounding box of the face in all frames and highlight the face for the first frame.
| In[3]:= |  X |
| Out[3]= |  |
Determine the regularized motion of the bounding box and trim all frames to the detected faces using a median bounding box size.
| In[4]:= | 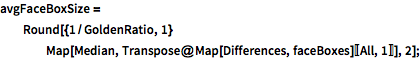 X |
| In[5]:= |  X |
| In[6]:= | X |
Determine the face-shifts with respect to the first frame and stabilize the video by undoing the shifts.
| In[7]:= |  X |
| In[8]:= |  X |
Determine the average skin probability distribution in the face bounding box using a typical skin classifier based on Lab color to detect facial skin.
| In[9]:= | X |
| In[10]:= | X |
| In[11]:= | X |
| Out[11]= |  |
For each frame, extract from all pixels the average Lab colors weighted by the above skin probability distribution.
| In[12]:= | X |
| In[13]:= | X |
| Out[13]= | 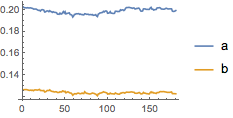 |
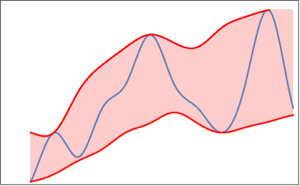
Find the optimal demixing angle α by searching for a signal with the least differential volatility.
| In[14]:= |  X |
| Out[14]= |
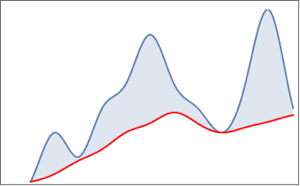
Extract the optimal pulse signal and regularize the pulse signal with a bandpass filter that selects frequencies between 0.5Hz and 3Hz.
| In[15]:= | X |
| In[16]:= | X |
| In[17]:= | X |
| Out[17]= | 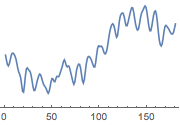 |
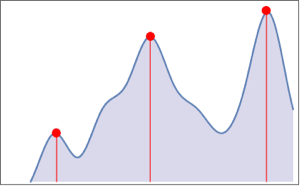
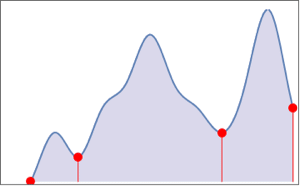
Extract the heart beats using FindPeaks.
| In[18]:= | X |
| Out[18]= |  |
| In[19]:= |  X |
| Out[19]= | 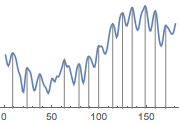 |
Convert the frame numbers into times and extract heart beat intervals.
| In[20]:= |  X |
| Out[20]= |
Median heart rate and its deviation.
| In[21]:= | X |
| Out[21]= |
| In[22]:= | X |
| Out[22]= |
| In[23]:= | X |
| Out[23]= |