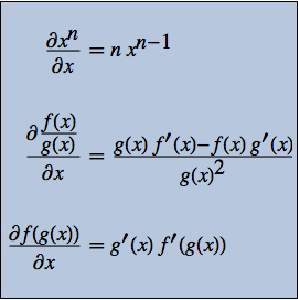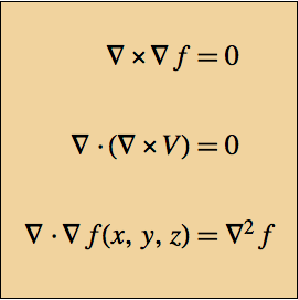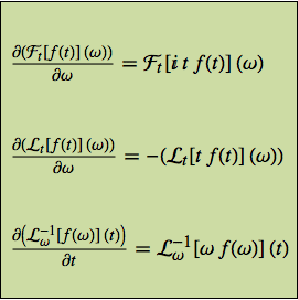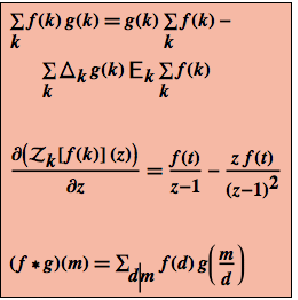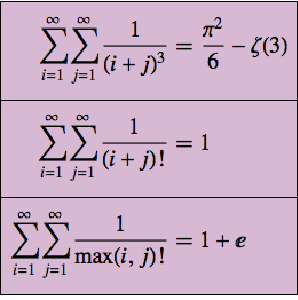Study Maxwell’s Equations
Derive the wave equation for a magnetic field from Maxwell's equations.
Enter Maxwell's equations in natural Lorentz–Heaviside units.
| In[1]:= | 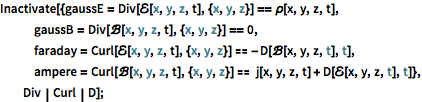 X |
Create a nicely formatted table of the equations.
| Out[2]//TraditionalForm= | |
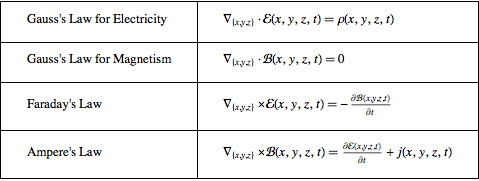 | |
Take the curl of Ampere's law in vacuum (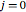 and
and 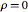 ).
).
| In[3]:= | X |
| Out[3]= |
Interchange order of differentiation.
| In[4]:= | X |
| Out[4]= |
Substitute Faraday's law.
| In[5]:= | X |
| Out[5]= |
Activating the equation results in the wave equation for the magnetic field.
| In[6]:= | X |
| Out[6]= |
This is the equation expressed using traditional notation.
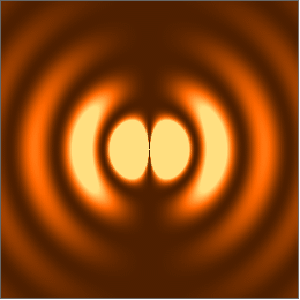
A plane-wave solution of the equation can be verified by a simple substitution.
| In[7]:= |  X |
| Out[7]= |