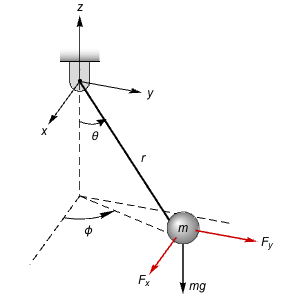
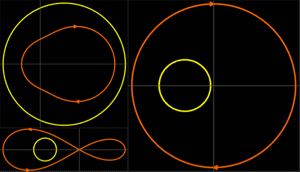
Estimator Design Using Feedback Linearization
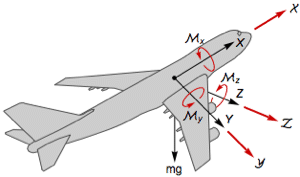
Feedback linearization also allows for the design of nonlinear estimators using linear techniques. Estimate the yaw angle 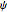 and the yaw rate
and the yaw rate 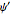 for a ship with hull length
for a ship with hull length  and speed
and speed 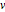 , based on Norrbin's model and using feedback linearization. »
, based on Norrbin's model and using feedback linearization. »
| In[1]:= | X |
| In[2]:= | 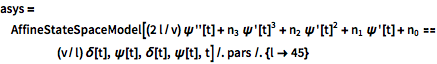 X |
| Out[2]= | 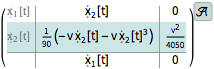 |
The model is completely feedback linearizable.
| In[3]:= | X |
| Out[3]= |
Compute a set of estimator gains using pole placement.
| In[4]:= | X |
| Out[4]= |
Assemble the nonlinear estimator.
| In[5]:= | X |
| Out[5]= | 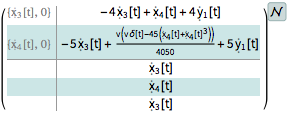 |
Plot the estimated state trajectories for a specific ship speed.
| In[6]:= | X |
| In[7]:= | X |
| In[8]:= | X |
| Out[8]= | 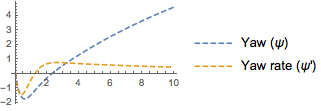 |
Compute the actual state trajectories.
| In[9]:= | X |
| Out[9]= |  |
Compare the actual and estimated yaw angles and yaw rates.
| In[10]:= |  X |
| Out[10]= |  |