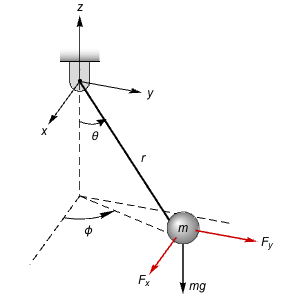
State-Space Transformation 

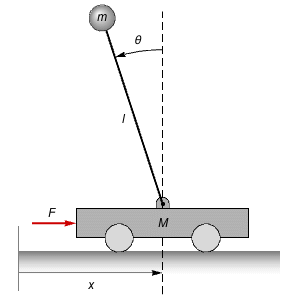
Obtain the governing equations of a spherical pendulum in Cartesian coordinates, put them into the affine state-space form, and convert them to spherical coordinates.

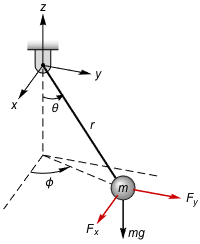The governing equations from the Lagrangian.

In[1]:=

X \[ScriptCapitalL] = 1/2 m (x'[t]^2 + y'[t]^2 + (x[t] x'[t] + y[t] y'[t])^2/( r^2 - x[t]^2 - y[t]^2)) + m g Sqrt[r^2 - x[t]^2 - y[t]^2];

In[2]:=

X Short[eqns = Table[D[D[\[ScriptCapitalL], q'[t]], t] - D[\[ScriptCapitalL], q[t]] == Subscript[F, q][t], {q, {x, y}}]]

Out[2]//Short=

The affine representation with states 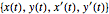and inputs .

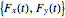In[3]:=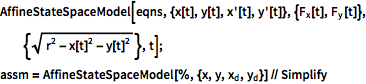

X Short[eqns = Table[D[D[\[ScriptCapitalL], q'[t]], t] - D[\[ScriptCapitalL], q[t]] == Subscript[F, q][t], {q, {x, y}}]]; AffineStateSpaceModel[ eqns, {x[t], y[t], x'[t], y'[t]}, {Subscript[F, x][t], Subscript[F, y][t]}, {Sqrt[r^2 - x[t]^2 - y[t]^2]}, t]; assm = AffineStateSpaceModel[%, {x, y, Subscript[x, d], Subscript[y, d]}] // Simplify

Out[3]=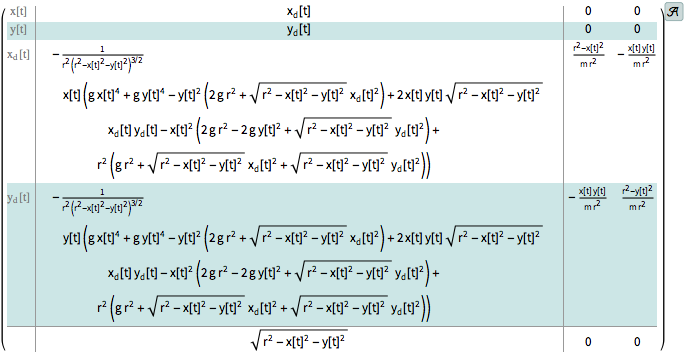

The transformation between spherical and Cartesian coordinates.

In[4]:=

X ctrans = Most@ CoordinateTransform[ "Spherical" -> "Cartesian", {r, \[Theta][t], \[Phi][t]}]

Out[4]=

The transformation of the coordinate derivatives.

In[5]:=

X ctransd = D[ctrans, t] /. {\[Theta]' -> Subscript[\[Theta], d], \[Phi]' -> Subscript[\[Phi], d]}

Out[5]=

The complete state transformation.

In[6]:=

X trans = Thread[{x[t], y[t], Subscript[x, d][t], Subscript[y, d][t]} -> Join[ctrans, ctransd]]

Out[6]=

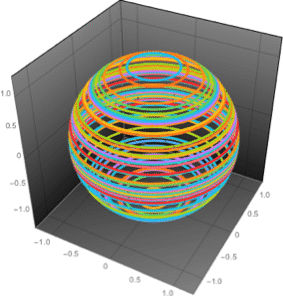
The expressions in spherical coordinates are much simpler.

In[7]:=

X StateSpaceTransform[ assm, {trans, {\[Theta][t], Subscript[\[Theta], d][t], \[Phi][t], Subscript[\[Phi], d][t]}}] // PowerExpand

Out[7]=