Control the Solution Process
Extract internal detail or intercept and control many aspects of the solution process.
Load the finite element package.
| In[1]:= | X |
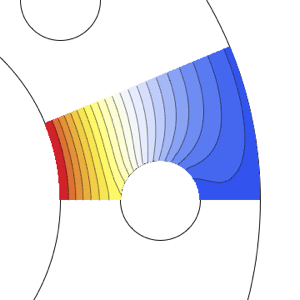
Specify a region and create a mesh with minimal bandwidth.
| In[2]:= |  X |
| Out[2]= |
Specify a plane strain operator.
| In[3]:= | 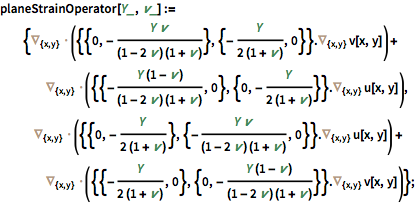 X |
Set up the equations.
| In[4]:= | 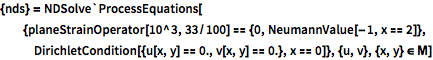 X |
| Out[4]= |
Inspect finite element data.
| In[5]:= | X |
| Out[5]= |
Extract the method data.
| In[6]:= | X |
| Out[6]= |
Extract the PDE coefficient data.
| In[7]:= | X |
| Out[7]= |
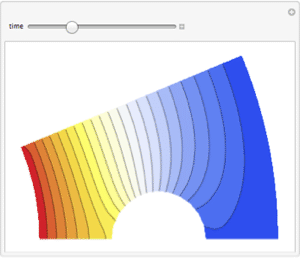
Extract the solution data.
| In[8]:= | X |
Discretize the PDE.
| In[9]:= | X |
| Out[9]= |
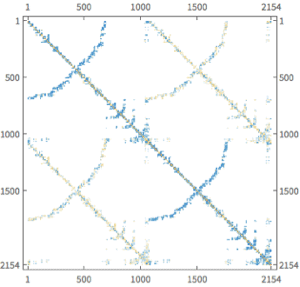
Extract and visualize the stiffness matrix.
| In[10]:= | X |
| Out[10]= | 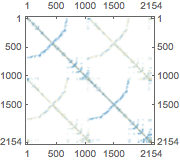 |