Mesh Regions
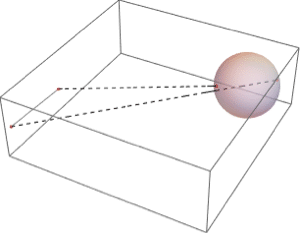
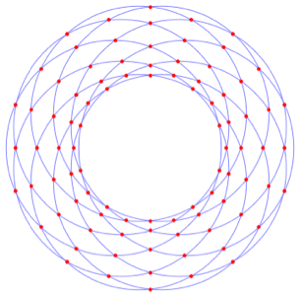
Mesh-based regions represent regions using simple special regions, called cells, such as point, line, triangle, and tetrahedron. MeshRegion represents the region as a disjoint union of simple cells. BoundaryMeshRegion represents a full-dimensional region using a ray-boundary intersection rule to define what points are in the region. Mesh-based regions are typically created by discretizing other regions or graphics or by automated construction from point sets. Mesh-based regions are what is traditionally called computational geometry.
Mesh regions in 1D.
| In[1]:= | X |
| Out[1]= |  |
| In[2]:= | X |
| Out[2]= |
Mesh regions in 2D.
| In[3]:= | X |
| Out[3]= | 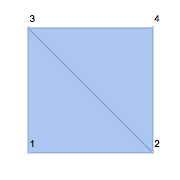 |
| In[4]:= | X |
| Out[4]= | 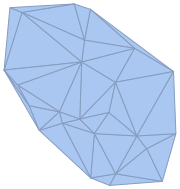 |
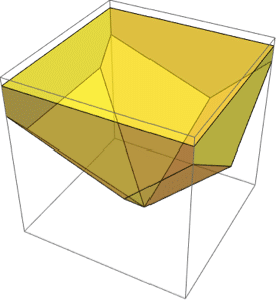
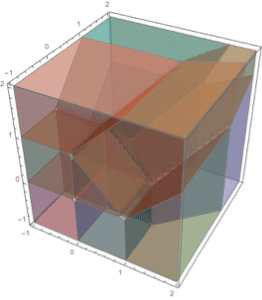
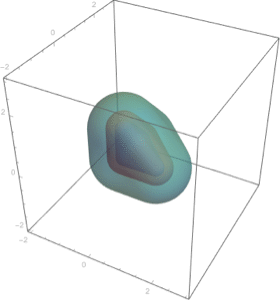
Mesh regions in 3D.
| In[5]:= |  X |
| Out[5]= | 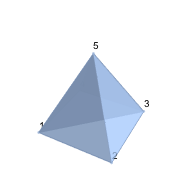 |
| In[6]:= | X |
| Out[6]= | 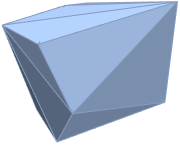 |
Boundary mesh region in 1D.
| In[7]:= | X |
| Out[7]= |  |
| In[8]:= | X |
| Out[8]= |
Boundary mesh regions in 2D.
| In[9]:= | X |
| Out[9]= | 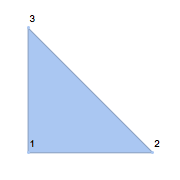 |
| In[10]:= | X |
| Out[10]= | 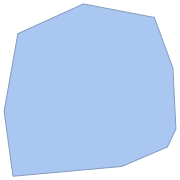 |
Boundary mesh regions in 3D.
| In[11]:= | 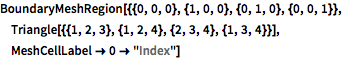 X |
| Out[11]= | 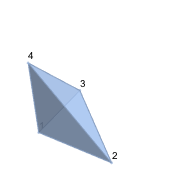 |
| In[12]:= | X |
| Out[12]= | 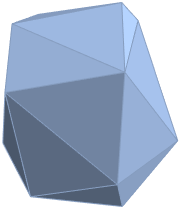 |