Verify Matrix Trigonometric Identities
Mathematica 9 includes algorithms for efficiently evaluating matrix functions. For a function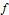 
with a power series 
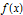for 
, the matrix function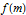 
for an 
×
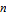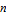matrix 
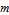is an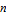 
×
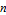matrix effectively based on the power series approximation using matrix powers of 
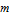, but can be computed more accurately and efficiently using advanced algorithms.
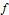with a power series 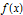for , the matrix function 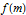for an 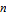× 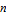matrix 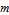is an 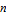× 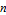matrix effectively based on the power series approximation using matrix powers of 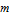, but can be computed more accurately and efficiently using advanced algorithms.In this example, the fundamental trig identities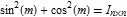 
and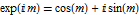 
will be tested for random matrices 
.
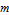| In[1]:= |  X |
Compute the matrix sine and cosine.
| In[2]:= |  X |
Show the magnitudes of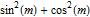 
and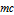 
.
| In[3]:= |  X |
| Out[3]= |  |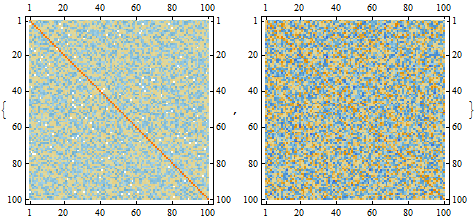
Theoretically, the plot on the left should just have the values along the diagonal. The noise that appears comes from numerical error and is actually quite small, but shows up because the logarithmic default color function used by MatrixPlot shows values with vastly different orders of magnitude.
Testing the error in the matrix norm shows the numerical error is quite small.
| In[4]:= |  X |
| Out[4]= |  |
| In[5]:= |  X |
| Out[5]= |  |