| |
The parameters, or synaptic weights as they are also called, are always
stored in the first element of a network, as described in 3.2.3: Network Format. The meaning of the individual
parameters is better explained in 13.1: Change the Parameter Values of an Existing Network.
Most neural networks can be evaluated on a symbolic input vector; then
the meaning of the parameters can be illustrated as in the example below.
Load the package.

Generate a network for demonstration purposes.
![fdfrwrd = InitializeFeedForwardNet[{{1, 1}}, {{2}}, {2},
RandomInitialization -> True, Neuron -> Tanh,
RandomInitialization -> True]](HTMLFiles/faq1_2.gif)
![FeedForwardNet[{{w1, w2}}, {Neuron -> Tanh,
FixedParameters -> None, AccumulatedIterations -> 0,
CreationDate -> {2003, 3, 4, 20, 53, 23},
OutputNonlinearity -> None, NumberOfInputs -> 2}]](HTMLFiles/faq1_3.gif)
The numerical values of the parameters are all placed in the first element
of the network.
![fdfrwrd[[1]]](HTMLFiles/faq1_4.gif)
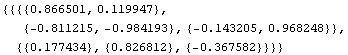
You can extract the first element and perform whatever process you want with
Mathematica.
An easy way to identify the meaning of the individual parameter is obtained by
applying the network to a symbolic input.
![fdfrwrd[{x1, x2}][[1]]](HTMLFiles/faq1_6.gif)
![-0.367582 + 0.826812 Tanh[0.968248 + 0.119947 x1 - 0.984193 x2] -
0.177434 Tanh[0.143205 - 0.866501 x1 + 0.811215 x2]](HTMLFiles/faq1_7.gif)
If you need to implement the trained network in, for example, a C program,
you might find the following command useful.
![fdfrwrd[{x1, x2}][[1]] // CForm](HTMLFiles/faq1_8.gif)
-0.36758202492667336 + 0.8268122850621071*
Tanh(0.9682476245672822 + 0.11994745409360652*x1 -
0.9841928909337702*x2) -
0.17743436966754977*Tanh(0.1432051850856072 -
0.866500737817343*x1 + 0.8112145157992191*x2)
|
| |
For most types of neural networks you concatenate the data sets into one set
before the training. This is shown in the first example below. For dynamic
neural networks, neural ARX and neural AR, it is slightly more complicated
because the individual data items are correlated. How you manage in this case
is shown in the second example.
Nondynamic Neural Networks
The general data format is described in 3.2.1: Data Format.
Load the package.

Generate a network for demonstration purposes.

In this data file, the input and output matrices are assigned to the variable
names x and y respectively. Once the data set has been loaded,
you can query the data using Mathematica commands. To better
understand the data format and variable name assignment, you may also want
to open the data file itself.
Load a data file containing input data x and output data y.
Show the contents of the input and output matrices.

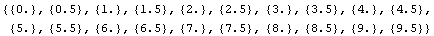
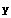

Check the number of data items and the number of inputs and outputs for each.
![Dimensions[x] Dimensions[y]](HTMLFiles/faq2_9.gif)
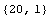
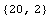
There are 20 data samples; the input has one dimension, and the output has
two. Introduce a second data set.
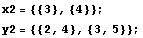
The dimensionality of the input and output must be the same in the two data
sets.
![Dimensions[x2]
Dimensions[y2]](HTMLFiles/qa_13.gif)
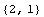
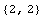
A new, joined data set can now be constructed by concatenating the two input
data sets, and similarly with the output data sets.
![xnew = Join[x, x2]](HTMLFiles/qa_16.gif)
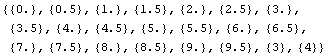
![ynew = Join[y, y2]](HTMLFiles/qa_18.gif)

Now you can start training your network with the combined data set.
Dynamic Neural Networks
Data from dynamic systems are correlated, and if two data sets are
concatenated in the way described in the previous example, then a transient
is introduced in the data. This transient might be small and unimportant.
There is, however, a way to avoid the transient totally. What you have to
do is to build the regressor, described in 2.6: Dynamic Neural Networks, for the two data sets and
then concatenate the result.
Load some packages.
<<NeuralNetworks`
<<Statistics`ContinuousDistributions`
<<Graphics`MultipleListPlot`
For demonstration purposes, generate a first data set.
Ndata = 30;
u1 = RandomArray[NormalDistribution[0, 3], {Ndata, 2}];
x = FoldList[Function[{xs, uin}, {(uin[[1]] + uin[[2]] +
0.6 * xs[[1]] + 0.8 * xs[[2]])/(1 + xs[[3]]^2), 0.7 * xs[[2]] +
uin[[2]], xs[[1]]}], {0, 0, 5}, Drop[u1, -1]];
y1 = x[[All, {1, 2}]];
Check dimensions of input and output, and the number of data for the first
data set.
![Dimensions[u1]
Dimensions[y1]](HTMLFiles/qa_21.gif)
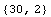
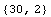
Generate a second data set.
Ndata = 20;
u2 = RandomArray[NormalDistribution[0, 3], {Ndata, 2}];
x = FoldList[Function[{xs, uin}, {(uin[[1]] + uin[[2]] +
0.6 * xs[[1]] + 0.8 * xs[[2]])/(1 + xs[[3]]^2), 0.7 * xs[[2]] + uin[[2]], xs[[1]]}], {0, 0, 5}, Drop[u2, -1]];
y2 = x[[All, {1, 2}]];
Check dimensions of input and output, and the number of data for the second
data set.
![Dimensions[u2]
Dimensions[y2]](HTMLFiles/qa_24.gif)
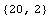
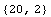
Choose the indices indicating the regressor, as described in
2.6: Dynamic Neural Networks.
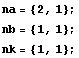
With one data set you can train a neural ARX model in the following way.
![{model1, fitrecord} =
NeuralARXFit[u1, y1, {na, nb, nk}, FeedForwardNet, {2}, 2];](HTMLFiles/qa_28.gif)
![[Graphics:HTMLFiles/qa_29.gif]](HTMLFiles/qa_29.gif)
With two data sets you have to do the following.
Generate the regressors and modified outputs of the two data sets.
![{x1, yy1} = MakeRegressor[u1, y1, {na, nb, nk}];
{x2, yy2} = MakeRegressor[u2, y2, {na, nb, nk}];](HTMLFiles/qa_30.gif)
Concatenate regressors and the modified outputs in the same way as in the
previous example.
![x = Join[x1, x2];
y = Join[yy1, yy2];](HTMLFiles/qa_31.gif)
Initialize a neural ARX model of your choice (by indicating nil training
iterations in NeuralARXFit).
![{model1, fitrecord} =
NeuralARXFit[u1, y1, {na, nb, nk}, FeedForwardNet,
{2}, 0, CriterionPlot -> False];](HTMLFiles/qa_32.gif)
Extract the feedforward or the RBF network in the first position of the
initialized neural ARX model (as described in
8.1.1: Initializing and Training Dynamic Neural Networks).
![ffrwd = model1[[1]]](HTMLFiles/qa_33.gif)
![FeedForwardNet[{{w1, w2}}, {AccumulatedIterations -> 0,
CreationDate -> {2003, 3, 4, 22, 30, 46},
Neuron -> Sigmoid, FixedParameters -> None,
OutputNonlinearity -> None, NumberOfInputs -> 5}]](HTMLFiles/qa_34.gif)
Train the feedforward or the RBF network.
![{ffrwd, fitrecord} = NeuralFit[ffrwd, x, y, 5];](HTMLFiles/qa_35.gif)
![[Graphics:HTMLFiles/qa_36.gif]](HTMLFiles/qa_36.gif)
Put back the trained network at the first position of the neural ARX model.
![model1[[1]] = ffrwd;](HTMLFiles/qa_37.gif)
You have now obtained a neural ARX model trained on both data sets. The
neural ARX model can be used, for example, to simulate the behavior of one
of the data sets.
![NetComparePlot[u1, y1, model1]](HTMLFiles/qa_38.gif)
![[Graphics:HTMLFiles/qa_39.gif]](HTMLFiles/qa_39.gif)
![[Graphics:HTMLFiles/qa_40.gif]](HTMLFiles/qa_40.gif)
|