Desarrollo de Software
Explore los detalles en el conjunto de Mandelbrot
Por el incremento en la velocidad computacional, las computaciones que pueden llevar mucho tiempo, ahora pueden hacerse en tiempo real.
Explore detalles del conjunto de Mandelbrot.
Dado que la computación es rápida, la visualización del resultado es interactiva.
Como se usa sintaxis de Mathematica, la velocidad de retorno es rápida.
| In[1]:= | 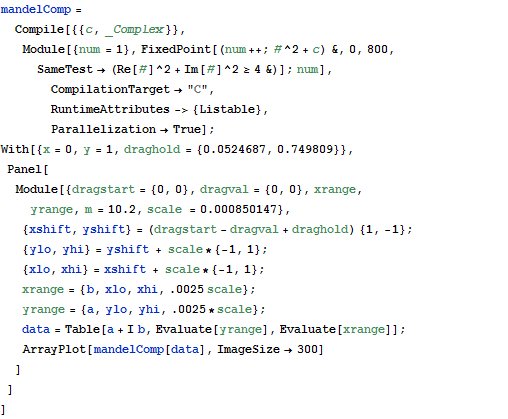 X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= | 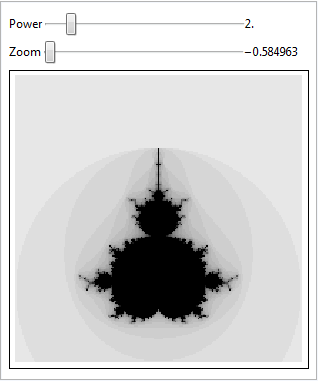 |