Core Algorithms
Stabilizer Chain for the 3x3x3 Rubik Group
Compute orders in a chain of stabilizer subgroups for the standard Rubik group with 48 moving facelets. The first group order is the number of configurations of the cube. The second group order is the number of configurations not moving facelet 1, then the number of configurations not moving facelets 1 and 3, etc. The last group in the chain is the identity group.
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= | 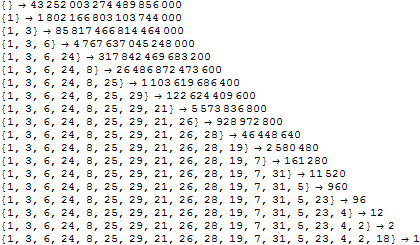 |
 |