Graphics & Visualization
Visualize Riemann Sums
Riemann summation uses discrete rectangles to approximate the area under a curve or volume under a surface.
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= |  X |
| Out[3]= | 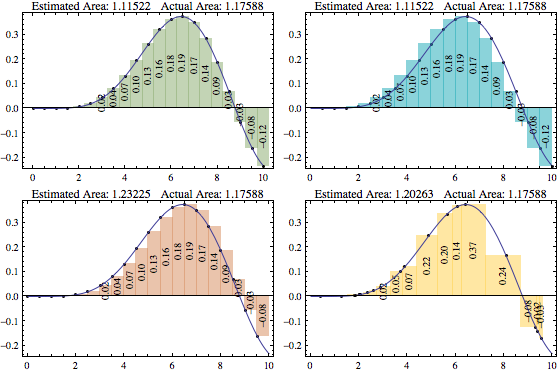 |
| New in Wolfram Mathematica 8: New and Improved Scientific and Information Visualization | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= |  X |
| Out[3]= |  |