Core Algorithms
Analyze Left-, Right-, and Interval-Censored Data
A comparison of two Kaplan-Meier estimates, using SurvivalDistribution, for some right-censored data and the mean residual life at 10 for the two groups.
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= | 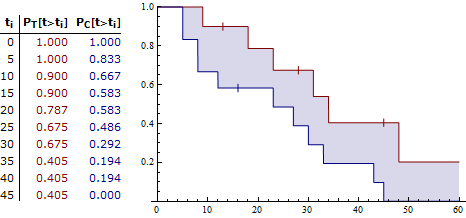 |
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |