Core Algorithms
Solve Optimization Problems in Density Estimation
Leverage the symbolic capabilities of KernelMixtureDistribution to solve for the least-squares cross-validation bandwidth. This method uses leave-one-out cross-validation to select a bandwidth that minimizes the integrated squared error of the resulting estimate.
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= | 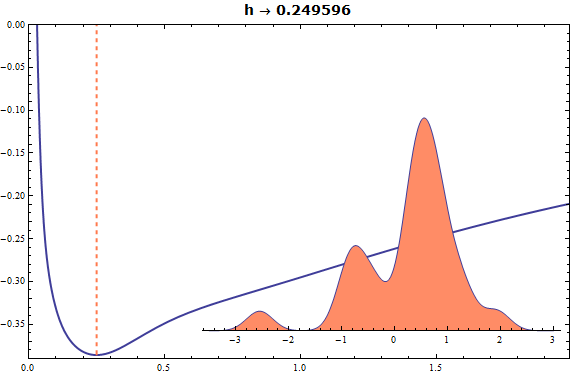 |