Core Algorithms
Use Stable Distribution to Model Stock Prices
Assuming daily logarithmic return of the stock market follows a stable distribution, simulate and visualize stock prices over a period of five years.
| In[1]:= | 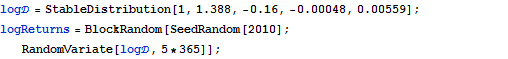 X |
| In[2]:= |  X |
| Out[2]= | 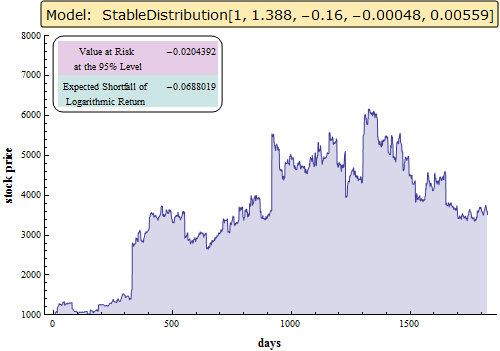 |
| New in Wolfram Mathematica 8: Parametric Probability Distributions | ◄ previous | next ► |
| In[1]:= | 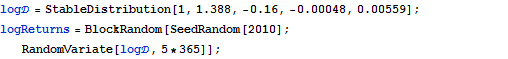 X |
| In[2]:= |  X |
| Out[2]= |  |