Heart Model 

In[10]:=

X phaselines1 = {Lighter[Red, .7], Table[Line[{{x, -1000}, {x, 1000}}], {x, times[[1]]}]}; phaselines2 = {Lighter[Red, .7], Table[Line[{{x, -1000}, {x, 1000}}], {x, times[[2]]}]}; phaselines3 = {Lighter[Red, .7], Table[Line[{{x, -1000}, {x, 1000}}], {x, times[[3]]}]}; phaselines4 = {Lighter[Red, .7], Table[Line[{{x, -1000}, {x, 1000}}], {x, times[[4]]}]};

In[11]:=

X phaselines = Join[phaselines1, phaselines2, phaselines3, phaselines4];

In[12]:=

X GraphicsGrid[{{Plot[sol[[1]], {t, 0, 1}, PlotRange -> {0, 40}, Epilog -> phaselines, PlotLabel -> x1], Plot[sol[[2]], {t, 0, 1}, PlotRange -> {0, .04}, Epilog -> phaselines, PlotLabel -> x2]}, {Plot[sol[[3]], {t, 0, 1}, PlotRange -> {0, 40}, Epilog -> phaselines, PlotLabel -> x3], Plot[sol[[4]], {t, 0, 1}, PlotRange -> All, Epilog -> phaselines, PlotLabel -> x4]}}, ImageSize -> 500]

Model a simplified beating heart with four state variables. The model and diagrams follow the paper:

M. E. Greene, J. W. Clark Jun., D. N. Mohr, and H. M. Bourland, "A Mathematical Model of Left-Ventricular Function," Medical and Biological Engineering, 11(2), 1973 pp. 126-134.

The left ventricle is a chamber of the heart that accepts oxygenated blood from the left atrium through the mitral valve. This oxygenated blood is then pumped through the aortic valve into the aorta. In the left ventricular model below, these components correspond to the atrial source pressure 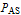, the mitral valve resistance 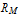, the aortic valve pressure 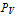, the aortic valve resistance 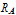, and the aortic root pressure .

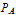The state variables in this model are the following.

Out[43]=

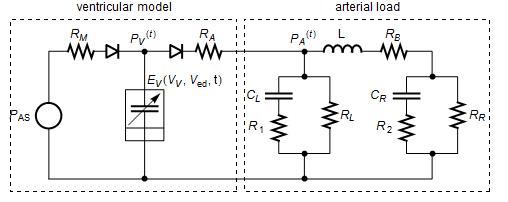
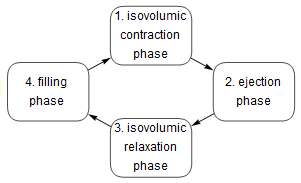
The cardiac cycle (heartbeat) is broken up into four phases. A simplification of the preceding model is used in each phase, depending upon which valves are closed.

Out[44]=

In each phase, depending on which valves are closed, a different variation of the model is used.

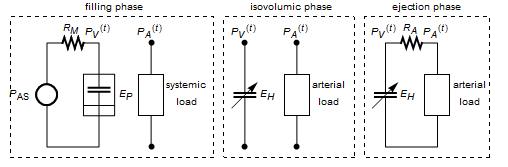Define the equations for 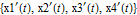during each phase of a heartbeat.

In[1]:=

X isoContractPhase = {(-x1[t] + Subscript[R, R] x4[t])/( Subscript[C, R] (Subscript[R, 2] + Subscript[R, R])), 0, (-x3[t] - Subscript[R, L] x4[t])/( Subscript[C, L] (Subscript[R, 1] + Subscript[R, L])), -x4[t]/ L (Subscript[R, B] + (Subscript[R, 1] Subscript[R, L])/( Subscript[R, 1] + Subscript[R, L]) + ( Subscript[R, 2] Subscript[R, R])/( Subscript[R, 2] + Subscript[R, R])) + (Subscript[R, L] x3[t])/( L (Subscript[R, 1] + Subscript[R, L])) - (Subscript[R, R] x1[t])/( L (Subscript[R, 2] + Subscript[R, R]))}; ejectionPhase = {(-x1[t] + Subscript[R, R] x4[t])/( Subscript[C, R] (Subscript[R, 2] + Subscript[R, R])), (-(Subscript[R, 1] + Subscript[R, L]) Subscript[E, V] x2[t] - Subscript[R, L] x3[t] - Subscript[R, 1] Subscript[R, L] x4[t])/Subscript[R, T], (Subscript[R, L] Subscript[E, V] x2[t] - (Subscript[R, L] + Subscript[R, A]) x3[t] - Subscript[R, L] Subscript[R, A] x4[t])/(Subscript[C, L] Subscript[R, T]), (-Subscript[R, R] x1[t])/( L (Subscript[R, 2] + Subscript[R, R])) + (Subscript[R, 1] Subscript[R, L] Subscript[E, V] x2[t] + Subscript[R, L] Subscript[R, A] x3[t] - (Subscript[R, 1] Subscript[R, L] Subscript[R, A] + Subscript[R, G] Subscript[R, T]) x4[t])/(Subscript[R, T] L)}; isoRelaxPhase = isoContractPhase; fillingPhase = {(-x1[t] + Subscript[R, R] x4[t])/( Subscript[C, R] (Subscript[R, 2] + Subscript[R, R])), (-Subscript[E, V] x2[t])/ Subscript[R, M] + Subscript[P, AS]/Subscript[R, M], (-x3[t] - Subscript[R, L] x4[t])/( Subscript[C, L] (Subscript[R, 1] + Subscript[R, L])), -x4[t]/ L (Subscript[R, B] + (Subscript[R, 1] Subscript[R, L])/( Subscript[R, 1] + Subscript[R, L]) + ( Subscript[R, 2] Subscript[R, R])/( Subscript[R, 2] + Subscript[R, R])) + (Subscript[R, L] x3[t])/( L (Subscript[R, 1] + Subscript[R, L])) - (Subscript[R, R] x1[t])/( L (Subscript[R, 2] + Subscript[R, R]))};

Elastance measures the ability of a stretched volume to recoil without change in pressure. In this model, the ventricular elastance has two phases, active and passive. The passive phase corresponds to the filling phase. During the active phase, the elastance is a function of both end diastolic volume 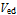and time. In the passive phase, the elastance depends only on the ventricular volume .

In[2]:=

X Subscript[a, 1][v_] := Piecewise[{{2.1*^-3 v^2 10^6 - 10^3 0.2338 v + 10.6, v <= 0.055}, {-1.0133*^-3 v^2 10^6 - 10^3 0.0626 v + 10.6, True}}]; Subscript[a, 2][v_] := Piecewise[{{150.0/1000, v <= 0.055}, {-6*v + 0.48, True}}]; Subscript[a, 3][v_] := Piecewise[{{2.8*^-3 v^2 10^6 - 10^3 0.3 v + 10.2, v <= 0.055}, {6.476*^-4 v^2 10^6 - 10^3 0.1816 v + 10.2, True}}]; Subscript[b, 1][v_] := -1.*^-4 v 10^3 + 0.0157; Subscript[b, 2][v_] := 45.0/1000; Subscript[b, 3][v_] := -4.*^-4 v 10^3 + 0.0431; Subscript[c, 1][v_] := 9.7*^-6 v^2 10^6 - 10^3 2.8*^-4 v + 0.12; Subscript[c, 2][v_] := 0.06; Subscript[c, 3][v_] := -40.2*^-6 v^2 10^6 + 10^3 4.78*^-3 v + 0.06; d = 100.0; f[v_, t_] := 1000 \!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(3\)]\( \(\*SubscriptBox[\(a\), \(i\)]\)[v] Exp[\(- \*SuperscriptBox[\((1000 \(\*SubscriptBox[\(b\), \(i\)]\)[v] \((t - \(\*SubscriptBox[\(c\), \(i\)]\)[v])\))\), \(2\)]\)]\)\) + d; activeElas = f[Subscript[V, ed], t - tstartelastance[t]] - f[Subscript[V, ed], 0] + 10^3 (10.6 Subscript[V, ed]^2 - 0.147 Subscript[V, ed] + 0.00234)/ Subscript[V, ed]; passiveElas = 10^3 (10.6 x2[t]^2 - 0.147 x2[t] + 0.00234)/x2[t];

Define the initial conditions and various model parameters.

In[3]:=

X xinit = {29, .0352, 30, .0047}; initconds = {{x1[0], x2[0], x3[0], x4[0]} == xinit, phase[0] == 1, tstartelastance[0] == 0}; heartParameters = {Subscript[R, A] -> 60, Subscript[R, M] -> 22}; arterialParameters = {Subscript[C, L] -> 2.35*^-4, Subscript[R, 1] -> 60, Subscript[C, R] -> 1.33*^-4, Subscript[R, 2] -> 300, Subscript[R, L] -> 12640, Subscript[R, B] -> 60, Subscript[R, R] -> 8550, L -> 21.9}; derivedParameters = {Subscript[R, T] -> Subscript[R, 1] Subscript[R, A] + Subscript[R, 1] Subscript[R, L] + Subscript[R, A] Subscript[R, L], Subscript[R, G] -> Subscript[R, B] (1 + Subscript[R, 2]/(Subscript[R, 2] + Subscript[R, R]))}; pressureParameters = {Subscript[P, V] -> x2[t] Subscript[E, V], Subscript[P, A] -> x3[t] + x3'[t] Subscript[C, L] Subscript[R, 1], Subscript[P, AS] -> 10}; params = Join[heartParameters, arterialParameters, derivedParameters, pressureParameters, {Subscript[V, ed] -> xinit[[2]]}];

Define parameters to be substituted into the equations for each phase. The elastances are generically named E_V in the equations. For the filling phase, substitute passive elastance for E_V. For all other phases, substitute active elastance.

In[4]:=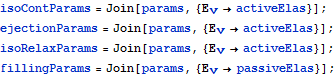

X isoContParams = Join[params, {Subscript[E, V] -> activeElas}]; ejectionParams = Join[params, {Subscript[E, V] -> activeElas}]; isoRelaxParams = Join[params, {Subscript[E, V] -> activeElas}]; fillingParams = Join[params, {Subscript[E, V] -> passiveElas}];

Substitute elastances and parameter values into the equations.

In[5]:=

X isoContractPhase = isoContractPhase //. isoContParams; ejectionPhase = ejectionPhase //. ejectionParams; isoRelaxPhase = isoRelaxPhase //. isoRelaxParams; fillingPhase = fillingPhase //. fillingParams;

The final system is piecewise defined across the four phases.

In[6]:=

X vars = {x1[t], x2[t], x3[t], x4[t]}; state = {isoContractPhase, ejectionPhase, isoRelaxPhase, fillingPhase}; eqns = { x1'[t] == Piecewise[Table[{state[[i, 1]], phase[t] == i}, {i, 1, 4}]], x2'[t] == Piecewise[Table[{state[[i, 2]], phase[t] == i}, {i, 1, 4}]], x3'[t] == Piecewise[Table[{state[[i, 3]], phase[t] == i}, {i, 1, 4}]], x4'[t] == Piecewise[Table[{state[[i, 4]], phase[t] == i}, {i, 1, 4}]] };

The transitions between the four phases outlined above are conditioned upon the relationship of the aortic valve pressure 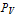, the atrial source pressure 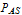, and the aortic root pressure .

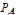In[7]:=

X ev1 = WhenEvent[ And[! (Subscript[P, AS] < Subscript[P, V] < Subscript[P, A]), phase[t] == 1], {phase[t] -> 2, Sow[t, 1]}] //. isoContParams; ev2 = WhenEvent[ And[! (Subscript[P, A] < Subscript[P, V]), phase[t] == 2], {phase[t] -> 3, Sow[t, 2]}] //. ejectionParams; ev3 = WhenEvent[ And[! (Subscript[P, AS] < 1.001 Subscript[P, V] < Subscript[P, A]), phase[t] == 3], {phase[t] -> 4, Sow[t, 3]}] //. isoRelaxParams; ev4 = WhenEvent[ And[! (1.001 Subscript[P, V] < Subscript[P, AS]), phase[t] == 4], {phase[t] -> 1, tstartelastance[t] -> t, Sow[t, 4]}] //. fillingParams;

In[8]:=

X events = {ev1, ev2, ev3, ev4};

Simulate the system.

In[9]:=

X {sol, times} = NDSolveValue[{eqns, initconds, events}, vars, {t, 0, 4}, DiscreteVariables -> {Element[phase, {1, 2, 3, 4}], tstartelastance[t]}] // Reap;

The different phases are separated by vertical lines.

Out[12]=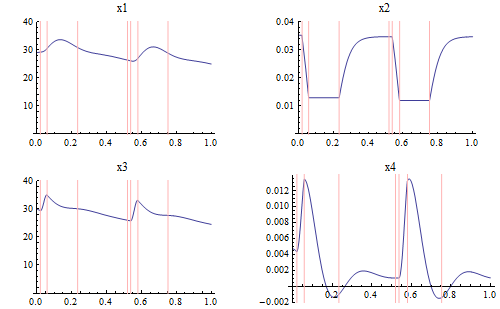