Transistor Amplifier Circuit
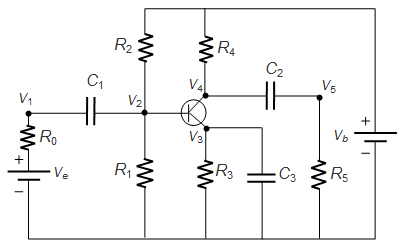
Model a transistor amplifier circuit that dispatches the voltage in a nonlinear fashion.
 X |
The input voltage varies sinusoidally. The circuit contains a transistor that modifies the voltage in a nonlinear way.
| In[1]:= | X |
Use Ohm's law and Kirchoff's current law to determine the governing equations for each node.
| In[2]:= | 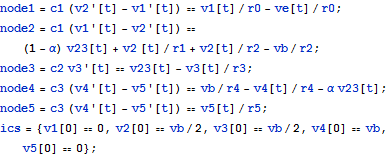 X |
Specify the parameters associated with the circuit.
| In[3]:= | 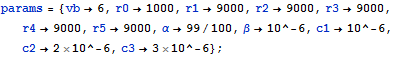 X |
Solve and visualize the system.
| In[4]:= |  X |
| In[5]:= | 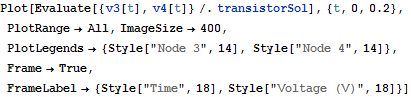 X |
| Out[5]= | 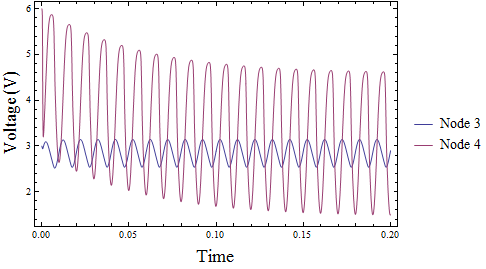 |