Electric Potential and Field of a Dipole
Mathematica 9 can not only compute in different coordinate systems but also transform between them. In this example, Mathematica computes an electric field from a potential in spherical coordinates, then transfroms to Cartesian coordinates to create a visualization.
Compute the electric field of a dipole from its potential and verify that it is a vacuum solution by computing the divergence:
| In[1]:= | X |
| Out[1]= |
| In[2]:= | X |
| Out[2]= |
| In[3]:= | X |
| Out[3]= |
Compute the equivalent fields in Cartesian coordinates for p=1 and visualize the equipotential surfaces and lines of force:
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
| In[6]:= |  X |
| In[7]:= | X |
| In[8]:= | X |
| Out[8]= | 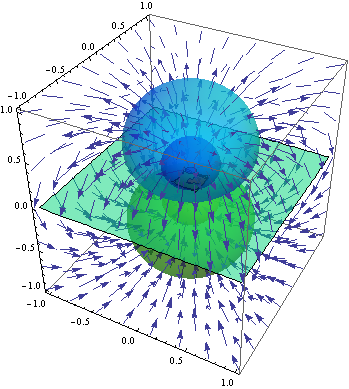 |