Design a Feedback Controller for a Mixing Tank 

The equations for a chemical's concentration in a mixing tank with two inflows and one outflow are Taylor linearized about an operating point to produce a descriptor state-space model.

In[1]:=

X eqns = {Derivative[1][v][t] == Subscript[q, 1][t] + Subscript[q, 2][t] - q[t], \!\( \*SubscriptBox[\(\[PartialD]\), \(t\)]\((c[t]\ v[t])\)\) == Subscript[c, 1] Subscript[q, 1][t] + Subscript[c, 2] Subscript[q, 2][t] - c[t] q[t], q[t] == Subscript[q, 0]/Sqrt[Subscript[v, 0]/A] Sqrt[v[t]/A]};

In[2]:=

X lsys = StateSpaceModel[ eqns, {{v[t], Subscript[v, 0]}, {c[t], (Subscript[c, 1] Subscript[q, 10] + Subscript[c, 2] Subscript[q, 20])/Subscript[q, 0]}, {q[t], Subscript[q, 0]}}, {{Subscript[q, 1][t], Subscript[q, 10]}, {Subscript[q, 2][t], Subscript[q, 20]}}, {q[t], c[t]}, t] /. Subscript[q, 0] -> Subscript[q, 10] + Subscript[q, 20] /. {Subscript[c, 1] -> 10., Subscript[c, 2] -> 20., Subscript[v, 0] -> 1000, Subscript[q, 10] -> 10., Subscript[q, 20] -> 20.}

Out[2]=

Because the system is of order 2, a feedback controller can assign two poles.

In[3]:=

X SystemsModelOrder[lsys]

Out[3]=

In[4]:=

X \[Kappa] = StateFeedbackGains[lsys, {-0.2, -0.15}]

Out[4]=

Obtain the closed-loop system.

In[5]:=

X csys = SystemsModelStateFeedbackConnect[lsys, \[Kappa]] // Chop

Out[5]=

The closed-loop system reacts considerably faster to changes than the uncompensated system.

In[6]:=

X res1 = OutputResponse[{csys, {0, 0.1, 0}}, {0, 0}, {t, 0, 175}]; res2 = OutputResponse[{lsys, {0, 0.1, 0}}, {0, 0}, {t, 0, 175}];

In[7]:=

X Plot[{res1, res2}, {t, 0, 175}, PlotStyle -> {Thick, Thick, Dashed, Dashed}, PlotRange -> All, ImageSize -> Medium]

Out[7]=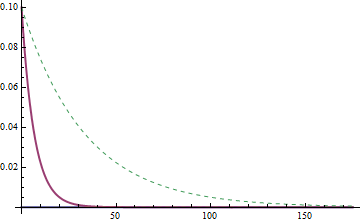