PID Tuning Rules
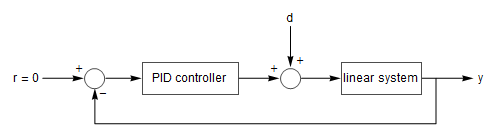 |
The process disturbance response using the Ziegler-Nichols tuning rule.
| In[1]:= |  X |
| Out[1]= |
| In[2]:= |  X |
| Out[2]= | 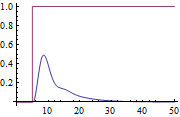 |
Use the Kappa-Tau rule.
| In[3]:= |  X |
| Out[3]= |
| In[4]:= |  X |
| Out[4]= | 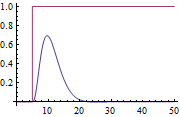 |
Use the AMIGO rule.
| In[5]:= | X |
| Out[5]= |
| In[6]:= |  X |
| Out[6]= | 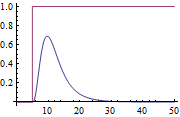 |
Use the Chien-Hrones-Reswick rule.
| In[7]:= |  X |
| Out[7]= |
| In[8]:= |  X |
| Out[8]= | 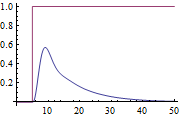 |
Use the Cohen-Coon rule.
| In[9]:= | 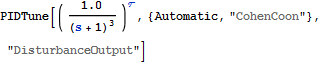 X |
| Out[9]= |
| In[10]:= |  X |
| Out[10]= | 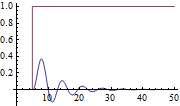 |
Use the Lambda Tuning rule.
| In[11]:= |  X |
| Out[11]= |
| In[12]:= |  X |
| Out[12]= | 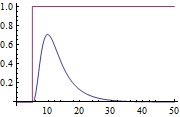 |
Use the Skogestad IMC rule.
| In[13]:= |  X |
| Out[13]= |
| In[14]:= |  X |
| Out[14]= | 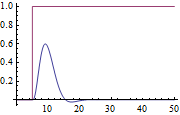 |
Use the Tyreus-Luyben rule.
| In[15]:= |  X |
| Out[15]= |
| In[16]:= |  X |
| Out[16]= | 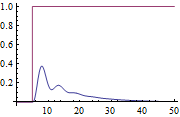 |