Fast Computation of Exact Sparse Null Spaces 

In[1]:=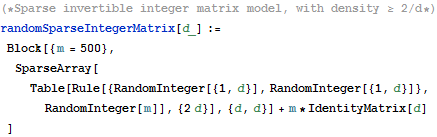

X (*Sparse invertible integer matrix model, with density \ \[GreaterEqual] 2/d*) randomSparseIntegerMatrix[d_] := Block[{m = 500}, SparseArray[ Table[Rule[{RandomInteger[{1, d}], RandomInteger[{1, d}]}, RandomInteger[m]], {2 d}], {d, d}] + m*IdentityMatrix[d] ]

In[2]:=

X m9s = {0.3120, 0.8784, 2.354, 3.652, 7.858, 13.33, 21.44}; m8s = {1.786, 4.713, 17.93, 39.93, 76.16, 108.5, 126.1}; mpl16s = {12.75, 38.79, 112.3, 223.1, 419.7, 612.9, 1150.};

In[3]:=

X (*Sparse invertible rational matrix model, with density \ \[GreaterEqual] 2/d*) randomSparseRationalMatrix[d_] := Block[{m = 500}, (SparseArray[ Table[Rule[{RandomInteger[{1, d}], RandomInteger[{1, d}]}, RandomInteger[m]], {2 d}], {d, d}] + m*IdentityMatrix[d])/ RandomInteger[{1, m}, {d, d}] ]

In[4]:=

X m9s = {0.2637, 2.599, 1.837, 3.711, 7.138, 15.24, 19.23}; m8s = {0.4211, 7.658, 25.98, 74.70, 138.9, 415.1, 343.9}; mpl16s = {6.148, 95.04, 174.1, 381.9, 672.8, 1226., 1884.};

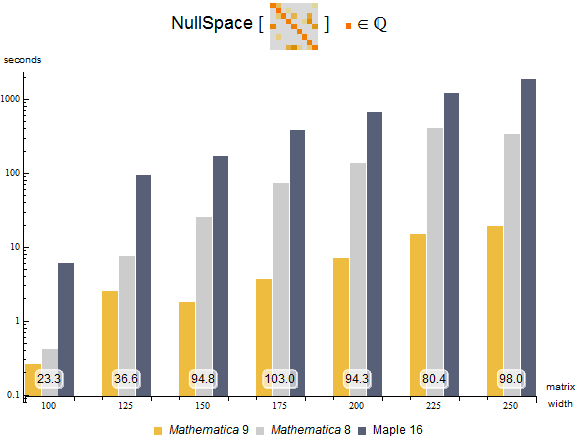
Shown are timings for computing the null space for square integer block sparse matrices. The experiment was performed on an Intel Xeon 3.07 GHz 64-bit Linux system, with a time limit of 3600 seconds. The number at the bottom tells how many times faster Mathematica 9 is than Maple 16.

Shown are timings for computing the null space for sparse square rational matrices.