Order Statistics Distribution for General Multivariate Distribution 

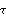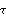A mission-critical service has three batteries with mean times to failure ₁, ₂, and 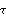₃. Dependencies of the failure times are assumed to be given by the Farlie-Gumbel-Morgenstern copula with parameter . Consider the event of the second battery's going out of order.

In[1]:=

X \[ScriptF]\[ScriptCapitalD] = OrderDistribution[ CopulaDistribution[{"FGM", \[Alpha]}, {ExponentialDistribution[ 1/Subscript[\[Tau], 1]], ExponentialDistribution[1/Subscript[\[Tau], 2]], ExponentialDistribution[1/Subscript[\[Tau], 3]]}], 2];

Compute the survival function, i.e. the probability for the system to be in order after epoch t.

In[2]:=

X sf[t_] = Refine[SurvivalFunction[\[ScriptF]\[ScriptCapitalD], t], t > 0] // Simplify

Out[2]=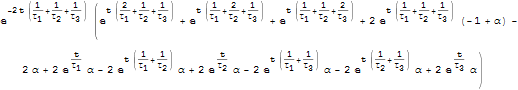

Find the expected time to failure.

In[3]:=

X mtf = (Mean[\[ScriptF]\[ScriptCapitalD]] // Simplify)

Out[3]=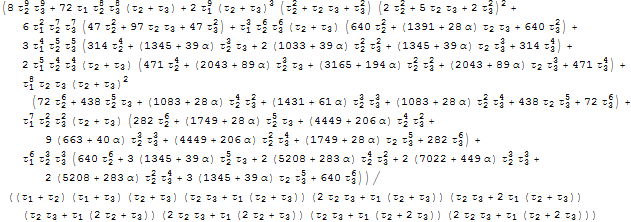

Plot the survival function for 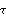₁=8.0, 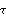₂=5, and 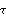₃=4.5 for different values of copula parameter .

In[4]:=

X Plot[sf[t] /. {Subscript[\[Tau], 1] -> 8.0, Subscript[\[Tau], 2] -> 5, Subscript[\[Tau], 3] -> 4.5} /. {{\[Alpha] -> -0.9}, {\[Alpha] -> 0}, {\[Alpha] -> 0.9}}, {t, 0, 8}, Evaluated -> True, ImageSize -> 400, PlotLegends -> {"\[Alpha] = -0.9", "\[Alpha] = 0", "\[Alpha] = 0.9"}]

Out[4]=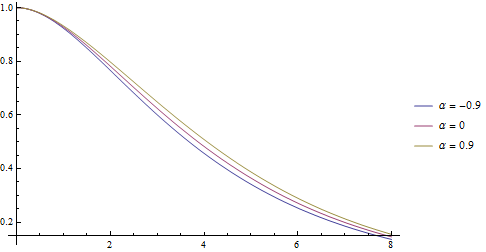