Eigenproblems
Find an eigenfunction for the finite square well eigenproblem 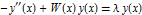 ,
, 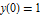 ,
, 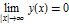 , where
, where 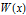 is a square well potential of height 5.
is a square well potential of height 5.
| In[1]:= |  X |
| Out[1]= | 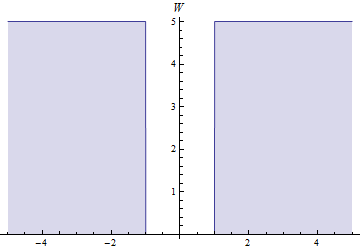 |
Start by plotting solutions of 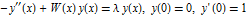 for
for 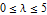 .
.
| In[2]:= | 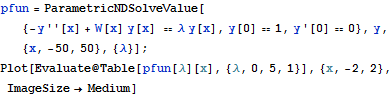 X |
| Out[2]= | 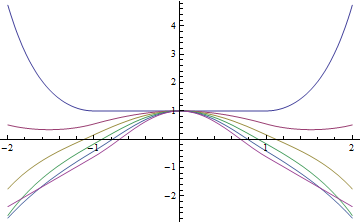 |
The true eigenfunctions satisfy 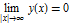 . These can be approximated by finding functions
. These can be approximated by finding functions 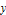 with
with 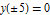 . Because the equation is symmetric in
. Because the equation is symmetric in 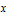 , only solutions with
, only solutions with 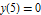 need to be found. Plot
need to be found. Plot 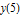 for
for 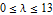 .
.
| In[3]:= | X |
| Out[3]= | 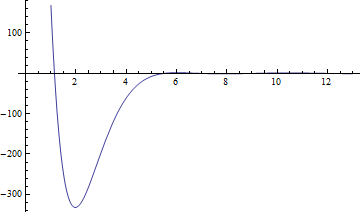 |
The root is the approximate eigenvalue.
| In[4]:= | X |
| Out[4]= |
Plot the approximate eigenfunction together with solutions for nearby  .
.
| In[5]:= |  X |
| Out[5]= | 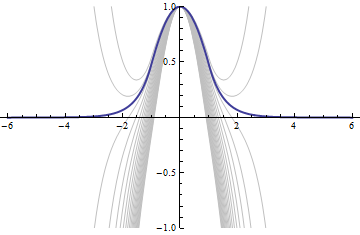 |