Резервное питание для атомных электростанций
| In[1]:= |  X |
| In[2]:= | 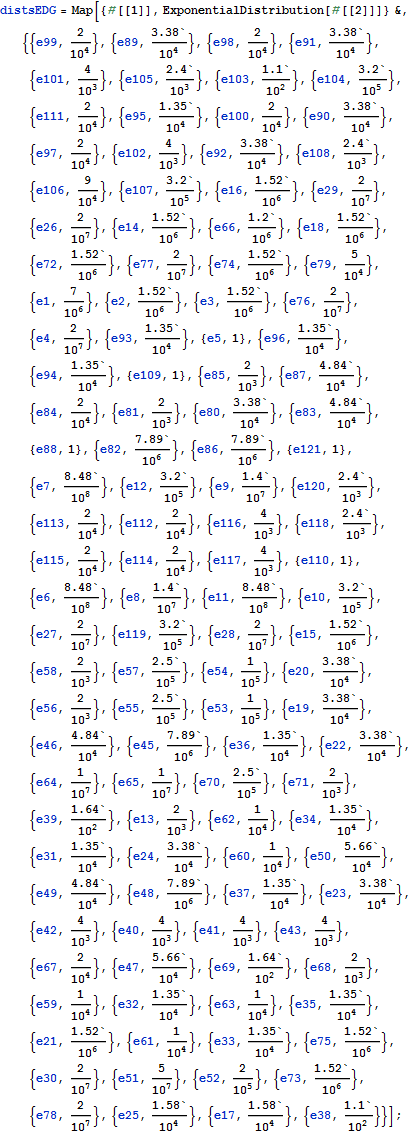 X |
Нахождение основых характеристик надёжности для дизельного генератора резервного питания.
| In[3]:= | X |
| In[4]:= |  X |
| Out[4]= |  |
Средняя продолжительность исправной работы в годах.
| In[5]:= | X |
| Out[5]= |