Надёжность автомобиля
Для исправной работы автомобиля необходимо, чтобы исправно работали колёса, мотор, передаточный механизм и один из двух тормозных механизмов.
| In[1]:= | 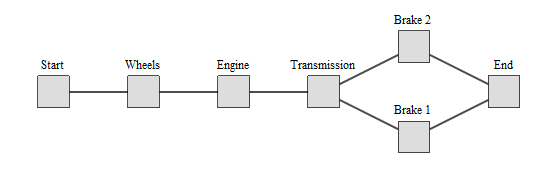 X |
| In[2]:= |  X |
Найдём функцию надёжности.
| In[3]:= | X |
| Out[3]= | 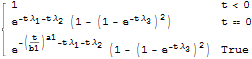 |
Без технического обслуживания, ожидаемая продолжительность исправной работы автомобиля приблизительно равняется трём годам.
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= |
Случайные реализации продолжительности исправной работы автомобиля.
| In[6]:= |  X |
| Out[6]= | 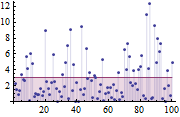 |