Надёжность запуска в космос
| In[1]:= | 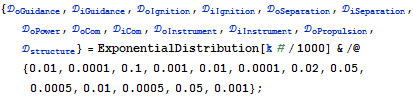 X |
| In[2]:= |  X |
| In[3]:= |  X |
| In[4]:= |  X |
| In[5]:= | X |
| In[6]:= |  X |
Моделируем процесс запуска в космос в виде трёхфазового процесса: наземная проверка, взлёт и работа на орбите. Эти три фазы имеют факторы экологической неблагоприятности, равные 5, 400 и 1.
| Out[6]= | 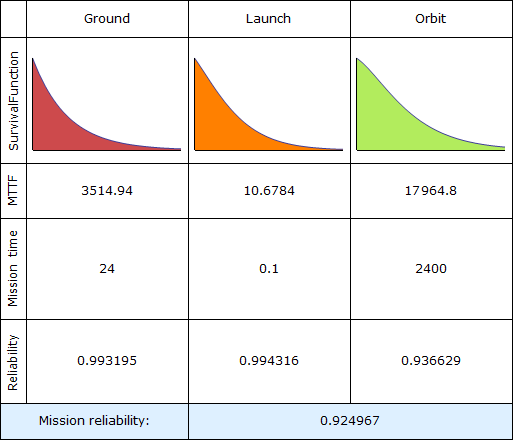 |