Clustering in Small-World Networks
Clustering can be used to quantify network robustness with respect to perturbation, and a high degree of clustering is one of the features captured by the small-world networks of Watts and Strogatz. In epidemiology, a robust network allows a disease to spread similarly even if the network is perturbed.
Compute the global clustering coefficient of a random graph.
| In[1]:= | X |
| Out[1]= | 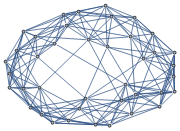 |
| In[2]:= | X |
| Out[2]= |
Compute the global clustering coefficients of a set of random graphs.
| In[3]:= |  X |
Create the heat map of selected graphs with respect to the coefficient values.
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | X |
| In[7]:= |  X |
| Out[8]= |  |