Стохастическое дифференциальное уравнение для экспоненциального затухания 

Зададим стохастический процесс, удовлетворяющий Итовскому стохастическому дифференциальному уравнению 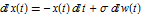. Оно моделирует экспоненциальное затухание в присутствии аддитивного Винеровского шума.

In[1]:=

X \[ScriptCapitalP] = ItoProcess[\[DifferentialD]x[ t] == -x[t] \[DifferentialD]t + \[Sigma] \[DifferentialD]w[t], x[t], {x, x0}, t, w \[Distributed] WienerProcess[]]

Out[1]=

Построение случайных реализаций траектории процесса при различных значениях параметра дисперсии .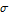

In[2]:=

X Table[ListLinePlot[ RandomFunction[\[ScriptCapitalP] /. {x0 -> 5}, {0, 4, 0.01}, 10], PlotLabel -> Row[{"\[Sigma]", "\[Equal]", N@\[Sigma]}]], {\[Sigma], {1/4, 1/2, 1, 2}}]

Out[2]=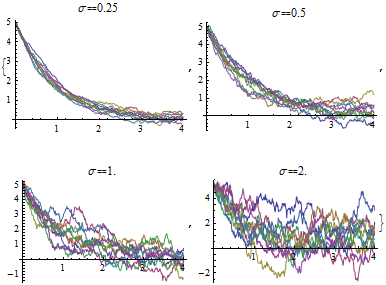

Функция среднего значения процесса 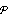не зависит от .

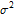In[3]:=

X Mean[\[ScriptCapitalP][t]]

Out[3]=

Это означает, что функция среднего значения совпадает с решением детерминистического уравнения.

In[4]:=

X x[t] /. DSolve[{x'[t] == -x[t], x[0] == x0}, x[t], t]

Out[4]=

Нахождение функции дисперсии процесса .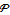

In[5]:=

X Variance[\[ScriptCapitalP][t]]

Out[5]=

Функция плотности вероятностей для значения процесса .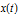

In[6]:=

X PDF[\[ScriptCapitalP][t], x]

Out[6]=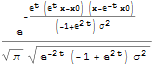