| New in Wolfram Mathematica 6: Dynamic Graphical Input | ◄ previous | next ► |
Use Forms Directly as Evaluatable Input
Mathematica 6 lets you create arbitrary forms, which can then be used as input—evaluating immediately to the settings they are given.
In[1]:= | {\!\(\*
TagBox[
DynamicModuleBox[{$CellContext`f$$ =
Sin[$CellContext`x^2], $CellContext`min$$ =
0, $CellContext`max$$ = 2 Pi},
InterpretationBox[
PanelBox[
TagBox[GridBox[{
{
StyleBox["\<\"Instant Plot\"\>",
StripOnInput->False,
FrontFaceColor->RGBColor[0.6, 0., 0.],
BackFaceColor->RGBColor[0.6, 0., 0.],
GraphicsColor->RGBColor[0.6, 0., 0.],
FontWeight->Bold,
FontSlant->Italic,
FontColor->RGBColor[0.6, 0., 0.]], "\[SpanFromLeft]"},
{"\<\"function:\"\>",
InputFieldBox[Dynamic[$CellContext`f$$]]},
{"\<\"min:\"\>",
InputFieldBox[Dynamic[$CellContext`min$$]]},
{"\<\"max:\"\>",
InputFieldBox[Dynamic[$CellContext`max$$]]}
}],
"Grid"]],
Plot[$CellContext`f$$, {$CellContext`x, $CellContext`min$$, \
$CellContext`max$$}]],
DynamicModuleValues:>{}],
Setting[#, {0}]& ]\), \[Integral]Sin[x^2] \[DifferentialD]x, \!\(\*
TagBox[
DynamicModuleBox[{$CellContext`f$$ =
Sin[$CellContext`x] + Sin[5 $CellContext`x], $CellContext`min$$ =
0, $CellContext`max$$ = 10 Pi},
InterpretationBox[
PanelBox[
TagBox[GridBox[{
{
StyleBox["\<\"Instant Plot\"\>",
StripOnInput->False,
FrontFaceColor->RGBColor[0.6, 0., 0.],
BackFaceColor->RGBColor[0.6, 0., 0.],
GraphicsColor->RGBColor[0.6, 0., 0.],
FontWeight->Bold,
FontSlant->Italic,
FontColor->RGBColor[0.6, 0., 0.]], "\[SpanFromLeft]"},
{"\<\"function:\"\>",
InputFieldBox[Dynamic[$CellContext`f$$]]},
{"\<\"min:\"\>",
InputFieldBox[Dynamic[$CellContext`min$$]]},
{"\<\"max:\"\>",
InputFieldBox[Dynamic[$CellContext`max$$]]}
}],
"Grid"]],
Plot[$CellContext`f$$, {$CellContext`x, $CellContext`min$$, \
$CellContext`max$$}]],
DynamicModuleValues:>{}],
Setting[#, {0}]& ]\), \[Integral](Sin[x] +
Sin[5 x]) \[DifferentialD]x} |
Out[1]=  | 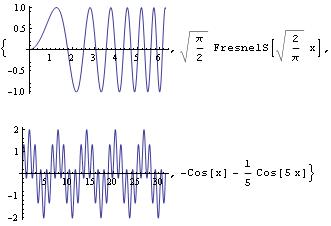 |