DC-DC Buck Converter 

Model a DC-to-DC buck converter from input voltage level vi to desired lower output voltage level vd using a pulse-width modulated feedback control q[t].

Play Animation » Stop Animation »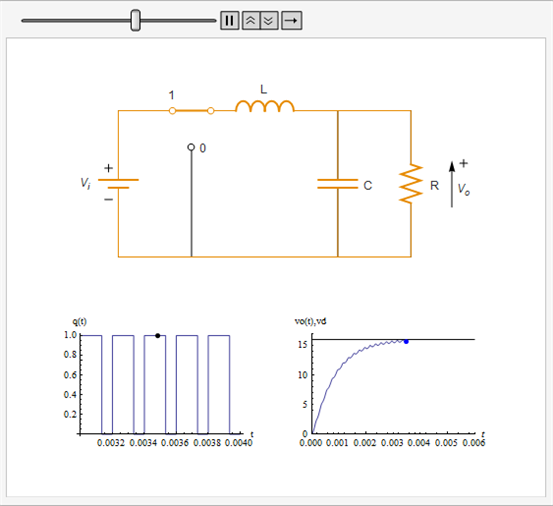

Use Kirchoff's laws to get a model for the circuit.

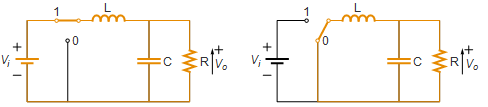In[1]:=

X system = {vo'[t] == -vo[t]/(r c) + i[t]/c , i'[t] == -vo[t]/l + q[t] vi/l, vo[0] == 0, i[0] == 0};

The control signal q[t] will switch the transistor on for a fraction vd/vi of each period .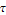

In[2]:=

X control = {q[0] == 1, WhenEvent[Mod[t, \[Tau]] == (vd/vi) \[Tau], q[t] -> 0], WhenEvent[Mod[t, \[Tau]] == 0, q[t] -> 1]};

Buck from a higher voltage vi=24 to a lower voltage vd=16.

In[3]:=

X pars = {vi -> 24, vd -> 16, r -> 22, l -> 2 10^-2, c -> 4 10^-6, \[Tau] -> 2 10^-4};

In[4]:=

X sol = NDSolve[{system, control} /. pars, {vo, i, q}, {t, 0, .01}, DiscreteVariables -> q, MaxSteps -> Infinity];

In[5]:=

X Row[{Plot[{vo[t] /. sol, vd /. pars}, {t, 0, .01}, PlotRange -> All, PlotLegends -> {"vo(t)", "vd"}], Spacer[50], Plot[q[t] /. sol, {t, 0, .001}, AxesLabel -> {t, q[t]}]}]

Out[5]=