Poincaré Sections 

Compute Poincaré sections using NDSolve with WhenEvent.

For a periodically driven planar example, the Poincaré section can be obtained by sampling at regular time intervals. Sampling can be done using WhenEvent, with an action having Sow with an enclosing Reap around the call to NDSolve.

Solve the Duffing equation 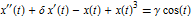and save samples at every period of the driving force, .

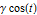In[1]:=

X data = Block[{\[Delta] = 0.15, \[Gamma] = 0.3}, Reap[NDSolve[{x''[t] + \[Delta] x'[t] - x[t] + x[t]^3 == \[Gamma] Cos[ t], x[0] == 0, x'[0] == 0, WhenEvent[Mod[t, 2 \[Pi]] == 0, Sow[{x[t], x'[t]}]]}, {}, {t, 0, 100000}, MaxSteps -> \[Infinity]]]][[-1, 1]];

The strange attractor for these parameter values can be visualized using ListPlot.

In[2]:=

X ListPlot[data, ImageSize -> Large, PlotRange -> {{-1.5, 1.5}, All}, PlotStyle -> PointSize[0.0025]]

Out[2]=

For higher-dimensional systems, the Poincaré section in effect samples on a slice across the phase space. This typically requires an event that depends on the solution. An example of this is the Arnold-Beltrami-Childress (ABC) flow that is used to model chaos in laminar flows of the three-dimensional Euler equations.

In[3]:=

X abc = {Derivative[1][x][t] == 3/4 Cos[y[t]] + Sin[z[t]], Derivative[1][y][t] == Cos[z[t]] + Sin[x[t]], Derivative[1][z][t] == Cos[x[t]] + 3/4 Sin[y[t]]};

The Poincaré section will be computed by taking samples as the solution crosses the 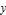plane. To get a full picture of the space, it will be necessary to use several different initial conditions.

In[4]:=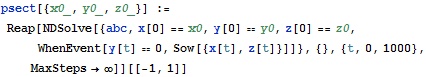

X psect[{x0_, y0_, z0_}] := Reap[NDSolve[{abc, x[0] == x0, y[0] == y0, z[0] == z0, WhenEvent[y[t] == 0, Sow[{x[t], z[t]}]]}, {}, {t, 0, 1000}, MaxSteps -> \[Infinity]]][[-1, 1]]

Apply the function to several initial conditions.

In[5]:=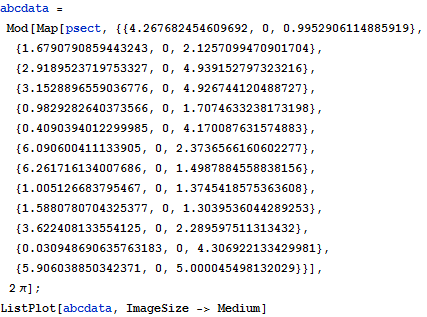

X abcdata = Mod[Map[psect, {{4.267682454609692, 0, 0.9952906114885919}, {1.6790790859443243, 0, 2.1257099470901704}, {2.9189523719753327, 0, 4.939152797323216}, {3.1528896559036776, 0, 4.926744120488727}, {0.9829282640373566, 0, 1.7074633238173198}, {0.4090394012299985, 0, 4.170087631574883}, {6.090600411133905, 0, 2.3736566160602277}, {6.261716134007686, 0, 1.4987884558838156}, {1.005126683795467, 0, 1.3745418575363608}, {1.5880780704325377, 0, 1.3039536044289253}, {3.622408133554125, 0, 2.289597511313432}, {0.030948690635763183, 0, 4.306922133429981}, {5.906038850342371, 0, 5.000045498132029}}], 2 \[Pi]]; ListPlot[abcdata, ImageSize -> Medium]

Out[5]=