Sampling Events 

In[2]:=

X ParametricPlot[{x[t], y[t]} /. sol1, {t, 0, 100}, Mesh -> points, MeshShading -> {Green, Orange}, PlotRange -> All, AxesLabel -> {x, y}]

In[4]:=

X Show[ParametricPlot[{x[t], y[t]} /. sol2, {t, 0, 100}, Mesh -> points, MeshShading -> {Green, Orange}, PlotRange -> All, AxesLabel -> {x, y}], ParametricPlot[{t, 1.1 Sin[5 t]}, {t, -1, 1}, PlotStyle -> Dashed]]

In[6]:=

X ParametricPlot[{x[t], y[t]} /. sol3, {t, 0, 100}, Mesh -> points, MeshShading -> {Green, Orange}, PlotRange -> All, AxesLabel -> {x, y}]

Mark the points where a solution crosses the 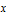axis.

In[1]:=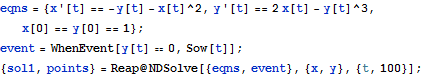

X eqns = {x'[t] == -y[t] - x[t]^2, y'[t] == 2 x[t] - y[t]^3, x[0] == y[0] == 1}; event = WhenEvent[y[t] == 0, Sow[t]]; {sol1, points} = Reap@NDSolve[{eqns, event}, {x, y}, {t, 100}];

Out[2]=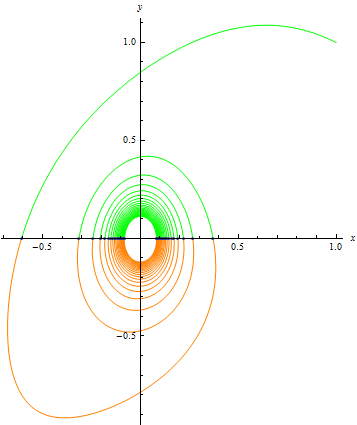

Mark the points where a solution crosses the graph of .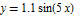

In[3]:=

X event = WhenEvent[y[t] == 1.1 Sin[5 x[t]], Sow[t]]; {sol2, points} = Reap@NDSolve[{eqns, event}, {x, y}, {t, 100}];

Out[4]=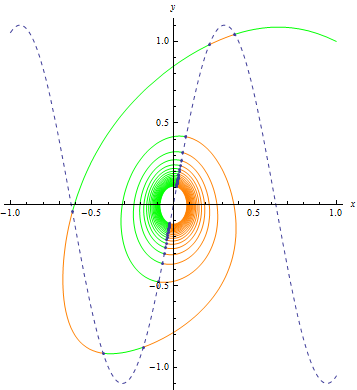

Mark the points where a solution has integer arc length.

In[5]:=

X aleqns = {p'[t] == Sqrt[ Derivative[1][x][t]^2 + Derivative[1][y][t]^2], p[0] == 0}; event = WhenEvent[Mod[p[t], 1] == 0, Sow[t]]; {sol3, points} = Reap@NDSolve[{eqns, aleqns, event}, {x, y, p}, {t, 100}];

Out[6]=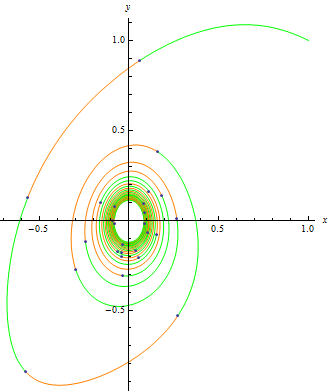