Efficiently Store Arrays with Symmetry
A new type of array allows you to specify and store only the independent components.
| In[1]:= | 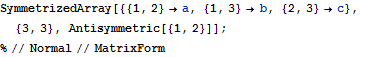 X |
| Out[1]//MatrixForm= |
For matrices, the only nontrivial symmetries are symmetry and antisymmetry, but for higher-rank arrays there are many more possibilities. The following figure illustrates some of them for a rank-4 array. Warm-colored squares represent independent components, with like-colored squares equal. Cold-colored squares are the negatives of the independent components, and white squares are forced to be zero by the symmetry.
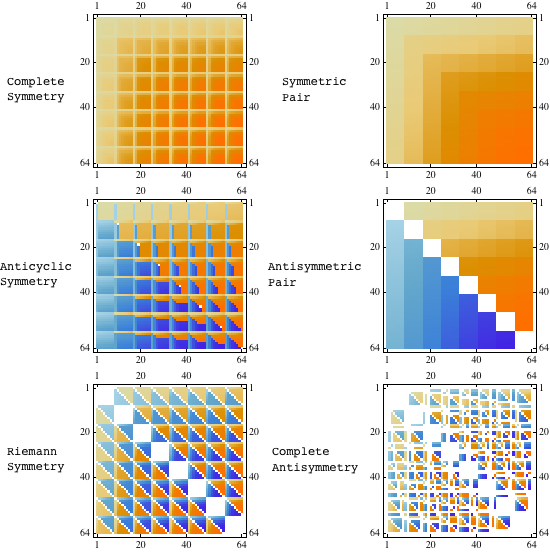 |
Storing only the independent components can produce enormous space savings.
| In[2]:= | 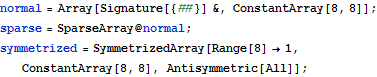 X |
| In[3]:= | X |
| Out[3]= |
| Out[3]= |
This allows exterior algebra computations in large dimensions—in this case a 4-form and 20-form in 25 dimensions.
| In[4]:= |  X |
| In[5]:= | X |
| Out[5]= |