Elastic Media in Spherical Coordinates
When an elastic medium is at equilibrium, the force at each point balances the divergence of the rank-2 stress tensor. The stress tensor, in turn, is the contraction of the symmetric rank-4 stiffness tensor and the rank-2 strain tensor. The strain tensor is the symmetrized gradient of the displacement field. All these fields can be represented and manipulated as symmetrized arrays, in any coordinate system known to Mathematica.
Define the stress tensor with built-in symmetry and compute its divergence in spherical coordinates.
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= | 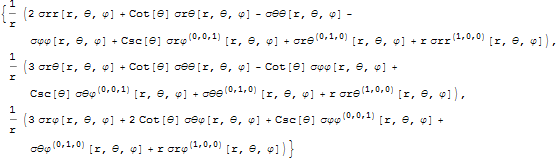 |
Compute the strain in spherical coordinates from its definition.
| In[3]:= | X |
| In[4]:= |  X |
| Out[4]= | 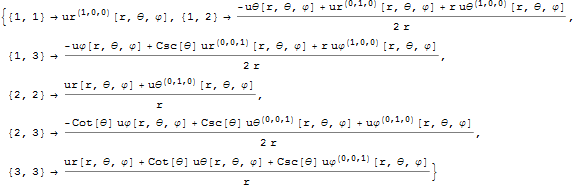 |
Contract the strain tensor with the stiffness tensor to obtain the stress tensor. Mathematica can verify the symmetry of the result.
| In[5]:= |  X |
| Out[5]= |
| Out[5]= |
| Out[5]= |