Approximate a Time-Delay Model 

A TransferFunctionModel with an delay in the denominator has infinitely many poles. TransferFunctionPoles can be used to plot all the poles in a given region.

In[1]:=

X tfm = TransferFunctionModel[{{{-20.}}, 30. - 20. E^(-s) + 0.1 s + s^2}, s, SamplingPeriod -> None];

In[2]:=

X delaypoles = Flatten@TransferFunctionPoles[tfm, {{-10, 10}, {-50, 50}}]; ListPlot[Table[{Re[p], Im[p]}, {p, delaypoles}], PlotMarkers -> {Automatic, 8}]

Out[2]=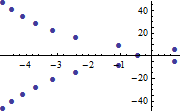

Use SystemsModelDelayApproximate to obtain delay-free approximations of time-delay systems. As the order is increased, the approximations converge to the original model.

In[3]:=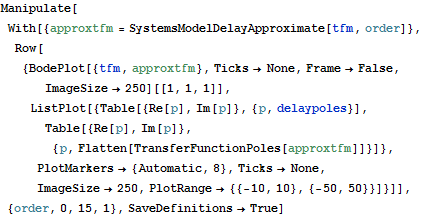

X Manipulate[ With[{approxtfm = SystemsModelDelayApproximate[tfm, order]}, Row[{BodePlot[{tfm, approxtfm}, Ticks -> None, Frame -> False, ImageSize -> 250][[1, 1, 1]], ListPlot[{Table[{Re[p], Im[p]}, {p, delaypoles}], Table[{Re[p], Im[p]}, {p, Flatten[TransferFunctionPoles[approxtfm]]}]}, PlotMarkers -> {Automatic, 8}, Ticks -> None, ImageSize -> 250, PlotRange -> {{-10, 10}, {-50, 50}}]}]], {order, 0, 15, 1}, SaveDefinitions -> True]

Out[3]=

Play Animation » Stop Animation »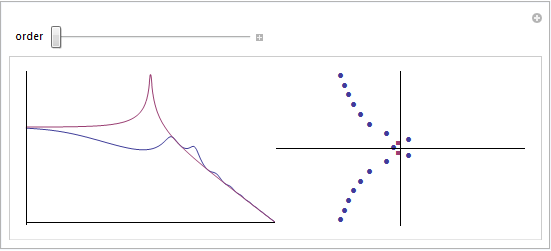