RLC Circuit Driven by a Periodic Signal and White Noise 

Consider an electrical circuit consisting of a resistor, inductor, and capacitor connected in series. The circuit is under external voltage, which is a superposition of a periodic signal and white noise.

In[1]:=

X CapacitorChargeModel = ItoProcess[{ \[DifferentialD]\[ScriptCapitalQ][t] == \[ScriptCapitalI][ t] \[DifferentialD]t, \[ScriptCapitalL] \[DifferentialD]\[ScriptCapitalI][ t] + \[ScriptCapitalR] \[ScriptCapitalI][ t] \[DifferentialD]t + 1/\[ScriptCapitalC] \[ScriptCapitalQ][t] \[DifferentialD]t == Sin[\[Omega] t] \[DifferentialD]t + \[Sigma] \[DifferentialD]w[ t]}, \[ScriptCapitalQ][ t], {{\[ScriptCapitalI], \[ScriptCapitalQ]}, {0, 0}}, t, w \[Distributed] WienerProcess[]]

Out[1]=

Define the parameters of the model.

In[2]:=

X params = {\[ScriptCapitalL] -> 2, \[ScriptCapitalC] -> 2, \[ScriptCapitalR] -> 1/2, \[Omega] -> 3/2, \[Sigma] -> 1/4};

Compute the mean function, i.e. the mean value of the charge of the capacitor as a function of time.

In[3]:=

X mqf = Simplify[Mean[CapacitorChargeModel[t] /. params]]

Out[3]=

Solve the deterministic problem in the absence of noise and compare it with the mean function.

In[4]:=

X detq = (Q[t] /. First[DSolve[\[ScriptCapitalL] Q''[t] + \[ScriptCapitalR] Q'[t] + Q[t]/\[ScriptCapitalC] == Sin[\[Omega] t] \[And] Q[0] == 0 && Q'[0] == 0 /. params, Q[t], t]]);

In[5]:=

X Simplify[detq == mqf]

Out[5]=

Compute the variance function.

In[6]:=

X vf = Simplify[Variance[CapacitorChargeModel[t] /. params]]

Out[6]=

Simulate the model using the strong Kloeden-Platen-Schurz scheme of order .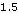

In[7]:=

X path = RandomFunction[ CapacitorChargeModel /. params, {0., 22., 0.002}, 12, Method -> "KloedenPlatenSchurz"]

Out[7]=

Visualize the simulated paths.

In[8]:=

X pls = ListLinePlot[path, PlotRange -> All, ImageSize -> 400]

Out[8]=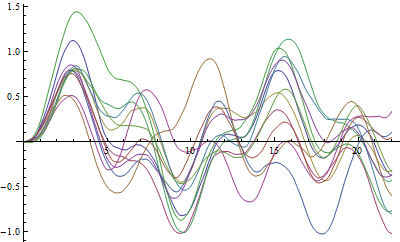

Visualize a 95% confidence band about the mean function.

In[9]:=

X epl = With[{q = Quantile[NormalDistribution[], (1 + .95)/2]}, Plot[{mqf - q Sqrt[vf], mqf, mqf + q Sqrt[vf]} /. params // Evaluate, {t, 0, 22}, PlotRange -> All, PlotStyle -> Directive[Thick, Black], FillingStyle -> Directive[Lighter[Blue, .5], Opacity[.15]], Filling -> {1 -> {3}}, ImageSize -> 400]]

Out[9]=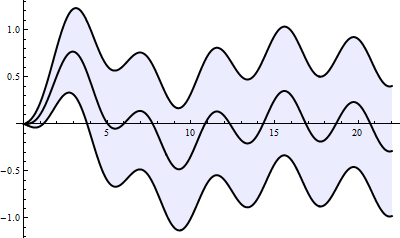

Combine the plots together.

In[10]:=

X Show[{epl, pls}, PlotRange -> All]

Out[10]=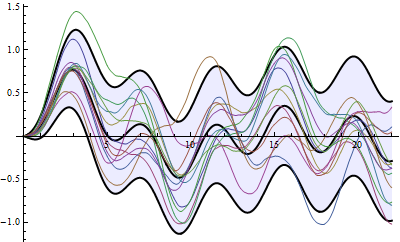