Simulate Zero Coupon Bond Using Chen's Model 

Define Chen's model for the evolution of interest rates.

In[1]:=

X chenmodel[\[Theta]_, \[Zeta]_, \[Beta]_, \[Eta]_, {r0_, \[Alpha]0_, \ \[Sigma]0_}] := ItoProcess[{ \[DifferentialD]r[ t] == (\[Theta] - \[Alpha][t]) \[DifferentialD]t + Sqrt[r[t]] \[Sigma][t] \[DifferentialD]w[t], \[DifferentialD]\[Alpha][ t] == (\[Zeta] - \[Alpha][t]) \[DifferentialD]t + Sqrt[\[Alpha][t]] \[Sigma][t] \[DifferentialD]w[t], \[DifferentialD]\[Sigma][ t] == (\[Beta] - \[Sigma][t]) \[DifferentialD]t + Sqrt[\[Sigma][t]] \[Eta] \[DifferentialD]w[t] }, r[t], {{r, \[Alpha], \[Sigma]}, {r0, \[Alpha]0, \[Sigma]0}}, t, w \[Distributed] WienerProcess[] ]

Visualize some trajectories using the stochastic Runge-Kutta method, correcting for negative interest rates that result from the use of the approximation.

In[2]:=

X ListLinePlot[ RandomFunction[chenmodel[1, 2, 1.2, 1, {1, 1, 1}], {0, 1, 0.01}, 6, Method -> {"StochasticRungeKutta", "ProjectionFunction" -> Function[{t, xvec}, Abs[xvec]]}], PlotRange -> All, ImageSize -> 300]

Out[2]=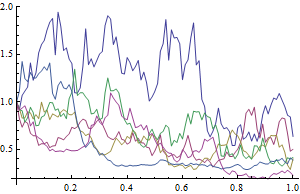

Evaluate zero-coupon bond maturing at time 1 using the Monte Carlo method. The present value of the bond is given by the mean of the process .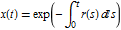

In[3]:=

X zcb[\[Theta]_, \[Zeta]_, \[Beta]_, \[Eta]_, {r0_, \[Alpha]0_, \ \[Sigma]0_}] = ItoProcess[\[DifferentialD]x[t] == r[t] \[DifferentialD]t, Exp[-x[t]], {x, 0}, t, r \[Distributed] chenmodel[\[Theta], \[Zeta], \[Beta], \[Eta], {r0, \[Alpha]0, \ \[Sigma]0}]];

In[4]:=

X td = RandomFunction[zcb[1, 2, 1.2, 1, {1, 1, 1}], {0, 1, 0.02}, 250, Method -> {"StochasticRungeKutta", "ProjectionFunction" -> Function[{t, xvec}, Abs[xvec]]}]; Plot[Mean[td[t]] // Evaluate, {t, 0, 1}, AxesOrigin -> {0, 0}, PlotLabel -> Row[{"P(0,1)\[TildeEqual]", Mean[td[1]]}]]

Out[4]=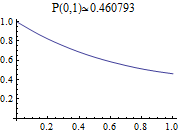