| New in Wolfram Mathematica 6: Real-Time 3D Graphics | ◄ previous | next ► |
Use Real-Time 3D Graphics as Input
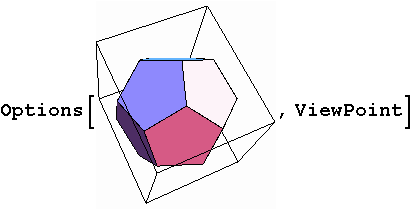
Mathematica 6 allows you to treat 3D graphics just like any other form of input to any computation.
In[1]:= | Options[\!\(\*
Graphics3DBox[
GraphicsComplex3DBox[
NCache[{{
0, 0, (Rational[
9, 8] + Rational[3, 8] 5^Rational[1, 2])^Rational[1, 2]}, {
0, 0, Rational[-1, 2] (
Rational[3, 2] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[1, 8] + Rational[-1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (-3 - 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[1, 8] + Rational[-1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (3 + 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (-1 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (1 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (-1 - 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (1 + 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {-(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[-1, 2], (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {-(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[
1, 2], (Rational[
1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[-1, 2],
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 2],
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {-(
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2], 0,
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (-1 - 5^Rational[1, 2]), (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (1 + 5^Rational[1, 2]), (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[
1, 2], 0, (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (-1 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (1 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Root[1 - 36 #^2 + 144 #^4& , 2, 0],
Rational[1, 4] (-3 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Root[1 - 36 #^2 + 144 #^4& , 2, 0],
Rational[1, 4] (3 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}}, {{
0, 0, 1.4012585384440737`}, {0, 0, -1.4012585384440737`}, {
0.17841104488654497`, -1.3090169943749475`,
0.46708617948135783`}, {0.17841104488654497`,
1.3090169943749475`, 0.46708617948135783`}, {
0.46708617948135783`, -0.8090169943749475, \
-1.0444364486709836`}, {0.46708617948135783`,
0.8090169943749475, -1.0444364486709836`}, {
1.0444364486709836`, -0.8090169943749475,
0.46708617948135783`}, {1.0444364486709836`,
0.8090169943749475,
0.46708617948135783`}, {-1.2228474935575286`, -0.5,
0.46708617948135783`}, {-1.2228474935575286`, 0.5,
0.46708617948135783`}, {
1.2228474935575286`, -0.5, -0.46708617948135783`}, {
1.2228474935575286`,
0.5, -0.46708617948135783`}, {-0.9341723589627157,
0, -1.0444364486709836`}, {-0.46708617948135783`, \
-0.8090169943749475, 1.0444364486709836`}, {-0.46708617948135783`,
0.8090169943749475, 1.0444364486709836`}, {
0.9341723589627157, 0,
1.0444364486709836`}, {-1.0444364486709836`, \
-0.8090169943749475, -0.46708617948135783`}, {-1.0444364486709836`,
0.8090169943749475, -0.46708617948135783`}, \
{-0.17841104488654494`, -1.3090169943749475`, -0.46708617948135783`}, \
{-0.17841104488654494`, 1.3090169943749475`, -0.46708617948135783`}}],
Polygon3DBox[{{15, 10, 9, 14, 1}, {2, 6, 12, 11, 5}, {5, 11, 7,
3, 19}, {11, 12, 8, 16, 7}, {12, 6, 20, 4, 8}, {6, 2, 13, 18,
20}, {2, 5, 19, 17, 13}, {4, 20, 18, 10, 15}, {18, 13, 17, 9,
10}, {17, 19, 3, 14, 9}, {3, 7, 16, 1, 14}, {16, 8, 4, 15,
1}}]],
ImageSize->{90., 104.12199652403548`},
ViewPoint->{-0.9624197700327529, -3.07580610224535, \
-1.031098932033377},
ViewVertical->{0.1306488041034501, -0.9156018302076686,
0.5053824851317418}]\), ViewPoint] |
Out[1]=  |