Text@TraditionalForm@

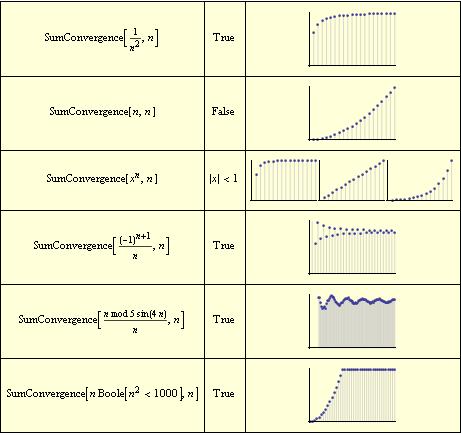
  Grid[{{HoldForm[\!\(TraditionalForm\`SumConvergence[

\*FractionBox[\(1\), 

SuperscriptBox[\(n\), \(2\)]], 

         n]\)], \!\(TraditionalForm\`SumConvergence[

\*FractionBox[\(1\), 

SuperscriptBox[\(n\), \(2\)]], n]\), DiscretePlot[\!\(TraditionalForm\`

\*UnderoverscriptBox[\(\[Sum]\), \(n\), \(m\)]

\*FractionBox[\(1\), 

SuperscriptBox[\(n\), \(2\)]]\), {m, 20}, ImageSize -> 100, 

      Ticks -> 

       None]}, {HoldForm[\!\(TraditionalForm\`SumConvergence[n, 

         n]\)], \!\(TraditionalForm\`SumConvergence[n, n]\), 

     DiscretePlot[\!\(TraditionalForm\`

\*UnderoverscriptBox[\(\[Sum]\), \(n\), \(m\)]n\), {m, 20}, 

      ImageSize -> 100, 

      Ticks -> None]}, {HoldForm[\!\(TraditionalForm\`SumConvergence[\*

FormBox[

SuperscriptBox["x", "n"],

TraditionalForm], n]\)], \!\(TraditionalForm\`SumConvergence[\*

FormBox[

SuperscriptBox["x", "n"],

TraditionalForm], n] // TraditionalForm\), 

     Row[Table[DiscretePlot[Sum[\!\(TraditionalForm\`

\*SuperscriptBox[\(x\), \(n\)]\), {n, m}], {m, 15}, ImageSize -> 75, 

        Ticks -> None], {x, \!\(TraditionalForm\`{

\*FractionBox[\(1\), \(3\)], 1, 

\*FractionBox[\(4\), \(3\)]}\)}]]}, \

{HoldForm[\!\(TraditionalForm\`SumConvergence[\*

FormBox[

FractionBox[

SuperscriptBox[

RowBox[{"(", 

RowBox[{"-", "1"}], ")"}], 

RowBox[{"(", 

RowBox[{"n", "+", "1"}], ")"}]], "n"],

TraditionalForm], n]\)], \!\(TraditionalForm\`SumConvergence[\*

FormBox[

RowBox[{"-", 

FractionBox[

SuperscriptBox[

RowBox[{"(", 

RowBox[{"-", "1"}], ")"}], "n"], "n"]}],

TraditionalForm], n]\), DiscretePlot[Sum[\!\(TraditionalForm\`

\*FractionBox[

SuperscriptBox[\((\(-1\))\), \((n + 1)\)], \(n\)]\), {n, m}], {m, 

       30}, ImageSize -> 100, 

      Ticks -> None]}, {HoldForm[\!\(TraditionalForm\`SumConvergence[\*

FormBox[

FractionBox[

RowBox[{

TemplateBox[{"n","5"},

"Mod"], " ", 

RowBox[{"sin", "(", 

RowBox[{"4", " ", "n"}], ")"}]}], "n"],

TraditionalForm], n]\)], \!\(TraditionalForm\`SumConvergence[\*

FormBox[

FractionBox[

RowBox[{

TemplateBox[{"n","5"},

"Mod"], " ", 

RowBox[{"sin", "(", 

RowBox[{"4", " ", "n"}], ")"}]}], "n"],

TraditionalForm], n]\), DiscretePlot[Sum[\!\(TraditionalForm\`\*

FractionBox[

RowBox[{

TemplateBox[{"n","3"},

"Mod"], " ", 

RowBox[{"sin", "(", 

RowBox[{"4", " ", "n"}], ")"}]}], "n"]\), {n, m}], {m, 20, 180, 2}, 

      ImageSize -> 100, Ticks -> None]}, {HoldForm[

      SumConvergence[n Boole[n^2 < 1000], 

       n]], \!\(TraditionalForm\`SumConvergence[\*

FormBox[

RowBox[{"n", " ", 

RowBox[{"Boole", "[", 

RowBox[{

SuperscriptBox["n", "2"], "<", "1000"}], "]"}]}],

TraditionalForm], n]\), DiscretePlot[\!\(TraditionalForm\`

\*UnderoverscriptBox[\(\[Sum]\), \(n\), \(m\)]n\ Boole[

\*SuperscriptBox[\(n\), \(2\)] < 1000]\), {m, 1, 80, 2}, 

      ImageSize -> 100, Ticks -> None]}}, Dividers -> All, 

   Background -> LightYellow, 

   Alignment -> {{Center, Center, Center}, Baseline}, 

   Spacings -> {1, 1.6}]