Wolframソリューション制御系制御系を構築,分析したり,設計について決定したことを記録したり,インタラクティブに制御装置を検証したりといった作業をすべて単一システムの中で行うことができます. Wolframの制御系ソリューションの基礎になっているのは,任意精度の数値計算,高性能の記号計算,高度な可視化,およびアルゴリズムの自動選択の機能を搭載した強力な記号と数値の計算用のハイブリッドエンジンであり,これらの機能すべてによって,正確な結果を効率的に得ることができます.Wolframソリューションは,アイディアを検証し,新しい系を効率的に設計するのに理想的なものです. |
 |
Wolframの強み
Wolframを使う理由
主な機能
Wolframテクノロジーには次のような何千もの組込み関数が含まれています.
- 微分方程式や差分方程式,および任意の代数制約条件で表される系の状態空間モデルを計算する
- 組込みの周波数応答ツールを使ったり,極を計算したり,リャプノフ方程式を解いたりして,系の安定性を分析する
- ブロック図の簡略化を使って,相互接続した部分を持つ系のモデルを簡略化する
- 伝達関数あるいは状態空間のオブジェクトとして線形モデルを操作する
- パラメータを変化させて系の動作をインタラクティブに分析する
- ボード(Bode)線図,ナイキスト(Nyquist)線図,ニコルス(Nichols)線図,根軌跡プロット等の古典的な技法を使う
- 系の可制御性と可観測性の特性を評価する
- 状態空間変換を計算して,可制御,可観測,最低,平衡のいずれかである分解を得る
- 分析と設計のために,離散時間系に相当する連続時間系を得る
- 力学系の性能をよくするフィードバック法則を開発する
- 時間遅延と代数方程式を含む系を設計し解析する
- 閉ループ伝達関数,PIDパラメータ化等を含む設計数量を自動的に計算する
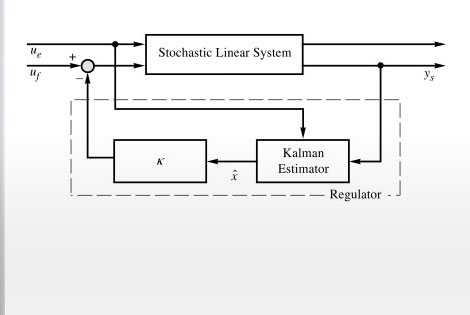
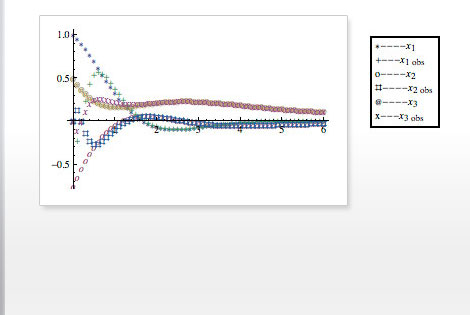
- 未測定の状態あるいはノイズのある測定を推測する
- さらにシミュレーションを行うための閉ループ系を形成するために,簡単に組み立てることができる制御装置と推定器のモデルを直接得る
- リアルタイム実装のための連続時間フィードバックアルゴリズムを離散化する
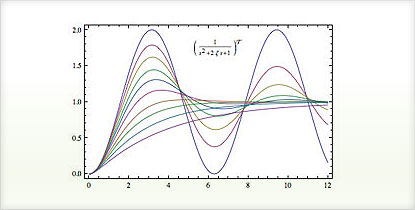
状態空間モデルあるいは伝達関数モデルの応答のシミュレーションを行う
組込み関数を使って系の安定性を測る
Wolframの強み
Wolframを使う理由
主な機能
現在お使いのツールには以下のような利点がありますか.
-
自然形式で伝達関数モデルと状態空間モデルを直接入力する
Matlabでは,伝達関数モデルを行ベクトルの行列としてのみ指定することができる -
記号系と数値号系を分析する
Matlabでは,数値系のみを扱うことが可能 -
確実に正確な結果を得るための完全に自動化された精度制御と任意精度演算
機械演算に依存するMatlabや他のシステムでは,数値的な確度の誤りにより重大なエラーが起ることがある -
さまざまな状況における制御系をインタラクティブに検証するために,インタフェースを即座に構築する
Wolframテクノロジー特有の機能 -
自由形式の言語入力によって,シンタックスを気にせずに結果を即座に出すことが可能
Wolframテクノロジー特有の機能 -
アルゴリズムの自動選択で正確な結果をすぐに得ることができる.さらに最適化するために計算途中で別のアルゴリズムに切り替えることも可能
Matlab等の他の計算システムでは,どの関数を適用するかを決めるために,方程式を手作業で分析する必要がある -
制御系機能は,Wolfram言語の中核システム,および信号処理,時系列,画像処理,ウェーブレット,線形代数等の20の組込みの応用分野にうまく統合されている
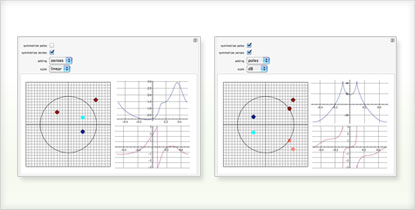
複素平面上の極と零点の集合から伝達関数を構築する
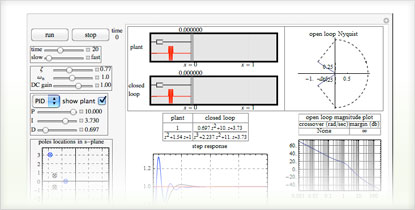
制御器と2次のプラントを持つフィードバック制御系のシミュレーションを行う
Wolframの強み
Wolframを使う理由
主な機能
Wolfram言語には,計算,モデル作成,可視化,開発,配備のための何千もの組込み関数が含まれています. »
制御系に特有の機能:
- 自然形式で状態空間モデルと伝達関数モデルを指定し,1つの形式から別の形式に簡単に変換を行う
- 微分方程式や差分方程式,および任意の代数制約条件で記述される系の線形の状態空間モデルを得る
- 広範囲に渡るアルゴリズムを使って連続時間と離散時間のモデル間で自由に変換する
- 一部分を選択,削除したり,一連のシステムを次々に繋げたり,部分システムの相互接続を構築したりといったシステム操作を行う
- ボード(Bode)線図,ナイキスト(Nyquist)線図,ニコルス(Nichols)線図,特異値プロットを中心に展開された周波数応答ツールを使って,系の分析と設計を行う
- 状態空間モデルを分析し,カルマン(Kalman),Jordan,平衡等さまざまな形式の実現間で変換を行う
- 時間遅延と代数方程式を持つモデルを含む,制御系の設計と解析のための統合機能 »
- PID制御器の自動調整 »
- ロバスト極配置のアルゴリズム,線形二次最適制御メソッド等の広範な種類のフィードバック設計ツールを使って,系の性能を改善する
- 開ループ系と閉ループ系のシミュレーションを行い,状態応答と出力応答を見極める
- Manipulateコマンドを使って,さまざまな状況における制御系をインタラクティブに分析する »
- 組込み関数を使ってRiccatiとリャプノフ(Lyapunov)の方程式を解く
- 特定データに簡単にアクセスするために,データベースに即座に接続する
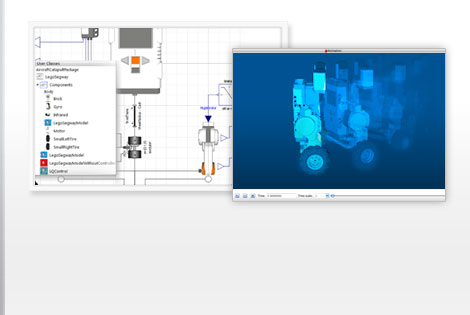
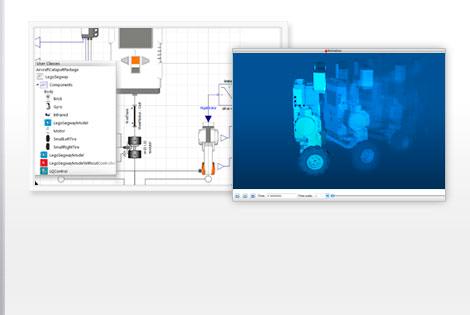
Wolfram SystemModeler は高忠実度モデリングのための物理モデリングとシミュレーションの最も完全なツールです.SystemModeler では次のようなことができます.
- 予め用意されたコンポーネントをドラッグアンドドロップするだけで,大規模なマルチドメインシステムのモデルを構築し,状態空間表現を導出し,モデルを評価することができる »
- 急激な変化や不連続性を持つ実際のシステムを設計しシミュレーションを実行する »
- Mathematica とシームレスに接続し,統合された究極のモデリング,シミュレーション,解析のワークフローを使う