Maximum-Volume Cuboid
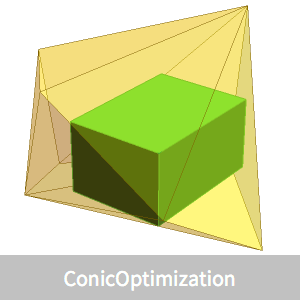
Find the maximum-volume axis-parallel cuboid inscribed in a convex polyhedron 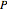 .
.
This example demonstrates how optimization of a product of positive terms can be expressed in terms of power-cone constraints that can be used with ConicOptimization to find the optimum.
Consider a random convex polyhedron  constructed as the convex hull of random points.
constructed as the convex hull of random points.
For the cuboid, find a lower-corner point 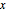 and a vector of side length
and a vector of side length 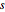 so that the cuboid is represented in the Wolfram Language by
so that the cuboid is represented in the Wolfram Language by 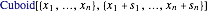 . The volume of the cuboid is just the product of the side lengths, so the objective is to maximize
. The volume of the cuboid is just the product of the side lengths, so the objective is to maximize 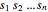 . If all of the corners of the cuboid are in
. If all of the corners of the cuboid are in 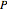 , then all of the points in the cuboid are also. The corners may be described by
, then all of the points in the cuboid are also. The corners may be described by 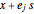 , where
, where 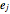 is in the set
is in the set 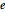 of all possible n‐tuples of elements from
of all possible n‐tuples of elements from 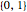 .
.
The problem becomes:
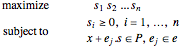
Since 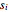 is non-negative, maximizing the product
is non-negative, maximizing the product 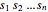 is the same as maximizing the geometric mean
is the same as maximizing the geometric mean 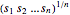 , which is known to be concave. Maximizing
, which is known to be concave. Maximizing 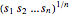 is equivalent to minimizing
is equivalent to minimizing 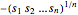 , which is convex. Using an auxiliary variable
, which is convex. Using an auxiliary variable 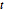 , reformulate the problem with a linear objective function -
, reformulate the problem with a linear objective function -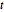 with the additional constraints
with the additional constraints 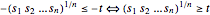 .
.
The problem becomes:
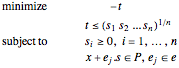
The power cone is the set of 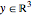 such that
such that 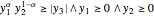 , and may be expressed in the Wolfram Language by
, and may be expressed in the Wolfram Language by 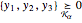 .
.
Since 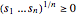 , the new constraint
, the new constraint 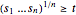 can be satisfied for non-negative
can be satisfied for non-negative 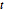 and is equivalent to
and is equivalent to 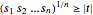 . This can be written as a series of power cone constraints
. This can be written as a series of power cone constraints
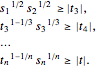
For 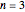 the problem becomes:
the problem becomes:
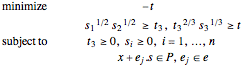
A convex polyhedron can be represented as intersections of half-spaces 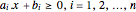 . Extract the coefficients
. Extract the coefficients 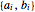 for each side.
for each side.
Solve the problem.
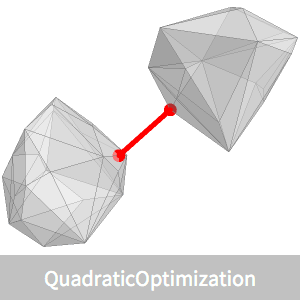
Show the maximum-volume-inscribed cuboid.
Instead of a polyhedron, take any convex conic representable set K⊆n—for example, an ellipsoid. A vertex of the cuboid 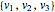 is inside the ellipsoid iff
is inside the ellipsoid iff 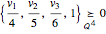 .
.
Solve the problem.
Plot the result.