The Wolfram Solution for Control Systems
Build and analyze control systems, document design decisions and interactively evaluate controllers–all in one system, with one integrated workflow.
Underlying the Wolfram control systems solution is a powerful hybrid symbolic-numeric computation engine with numerics of any precision, high-performance symbolics, advanced visualizations and automated algorithm selection–everything to get accurate results efficiently. The Wolfram solution is ideal for testing ideas and designing efficient and reliable control systems.
- The Wolfram Edge
- How Wolfram Compares
- Key Capabilities
Wolfram technologies include thousands of built-in functions that let you:
- Compute the state-space model of a system described by difference or differential equations and any algebraic constraints
- Analyze the stability of a system using built-in frequency-response tools, computing the poles or solving a Lyapunov equation
- Simplify models of systems with interconnected components using block-diagram reduction
- Manipulate linear models as transfer-function or state-space data objects
- Interactively analyze the system behavior as parameters are varied
- Employ classical techniques such as Bode, Nyquist, Nichols and root locus plots to analyze and design control systems
- Evaluate the controllability and observability properties of a system
- Compute state-space transformations to obtain decompositions that are controllable, observable, minimal or balanced
- Obtain continuous-time equivalents of discrete-time systems for analysis and design
- Develop feedback laws to enhance the performance of dynamic systems
- Design and analyze systems with time delays and algebraic equations
- Automatically compute design quantities including closed-loop transfer functions, PID parametrizations and more
- Estimate unmeasured states or noisy measurements
- Directly obtain models of controllers and estimators that can be easily assembled to form a closed-loop system for further simulations
- Discretize continuous-time feedback algorithms for real-time implementation
Does your current tool set have these advantages?
-
Directly input both transfer-function and state-space models in natural form
Matlab allows you to specify transfer-function models only as a matrix of row vectors -
Analyze symbolic and numeric systems
Matlab handles numeric systems only -
Fully automated precision control and arbitrary precision arithmetic to ensure accurate results
Matlab and other systems relying on machine arithmetic can show critical errors due to numerical accuracy failure -
Instant interface construction to test a control system interactively for different scenarios
Unique to Wolfram technologies -
Free-form linguistic input produces immediate results without the need for syntax
Unique to Wolfram technologies -
Automated algorithm selection to get accurate results quickly—sometimes switching mid-calculation for further optimization
Other computation systems like Matlab make you analyze your equations manually to determine which function to apply - Control systems functionality is well integrated with the core Wolfram Language and more than 20 built-in application areas, such as signal processing, time series, image processing, wavelets, linear algebra and more
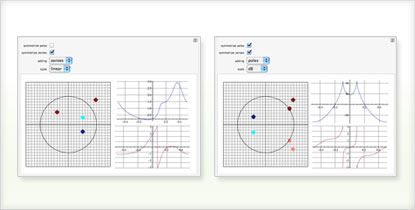
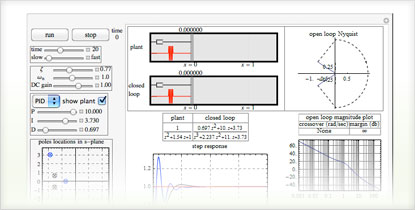
Control systems specific capabilities:
- Specify state-space and transfer-function models in natural form and easily convert from one form to another
- Obtain linearized state-space models of systems described by differential or difference equations and any algebraic constraints
- Freely convert between continuous-time and discrete-time models using a wide selection of algorithms
- Perform system manipulations, such as selecting or deleting subparts, cascading a set of systems, constructing interconnections of subsystems and more
- Analyze and design systems using frequency-response tools centered around Bode plot, Nyquist plot, Nichols plot and singular-value plot
- Analyze state-space models and convert between different realizations, including Kalman, Jordan, balanced and other forms
- Integrated functionality for designing and analyzing control systems, including models with time delays and algebraic equations »
- Automatic tuning of PID controllers »
- Improve the performance of systems using a broad selection of feedback design tools, such as robust pole-assignment algorithms and linear-quadratic optimal control methods
- Simulate open- and closed-loop systems to determine state and output responses
- Analyze a control system interactively for different scenarios using the Manipulate command »
- Solve Riccati and Lyapunov equations using built-in functions
- Connect to databases instantly for easy access to specialized data
Wolfram SystemModeler is the most complete physical modeling and simulation tool for high-fidelity modeling. With SystemModeler, you can:
- Build models of complex, multi-domain systems using simple drag-and-drop of ready-made components; derive the state-space representations; and evaluate the models »
- Design and simulate real-world systems that exhibit rapid changes or discontinuities »
- Connect seamlessly with Mathematica for the ultimate integrated modeling, simulation and analysis workflow



Consulting Solutions
Enlist the world’s computation experts to help with your project—any size, any level. At Wolfram, we know what’s possible with computational technology because we are global leaders in creating it. That gives us an unprecedented depth of expertise in applying it to consulting work in a variety of fields. Whether individual or enterprise, from concept to deployment, our computation experts can help you achieve robust results with less time and effort. Get us started with your project today




