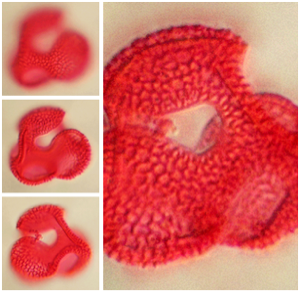
Vectorize a Bitmap Icon
ImageMesh converts foreground segments of a raster image into mesh regions encoded by polygons. By partitioning an image into color segments, you can then transcribe these constituents into polygons and reassemble them as a Graphics version of the original image. This process is called vectorization and constitutes the inverse of Rasterize.
An icon image to be vectorized.
img = \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztnQd4FNXax0M6oZO+u9mWQgsdUaqA9N4JJQQIvVdBOgiI9JZCr0oV9epV
uZbP67VcRS9NipQIKF0IhJIAIfO957wzZ86U3SSbQBRznpd5zk52l905v/2/
5ZyZsQ0Y03mwu5ub2wRf2HTuP7nx+PH9X+tSGh50Gz1h2JDRgwa2Gj1x0JBB
418a4AE7vxT/kb5Q2ApbYStsha2wFbbCVtgKW2ErbIWtsBW2wlbYClthK2z5
2n4+9nPC6jVDBw3q1KFjjSpVbaYwW5i50P4yZgqLLle+S6dO/ePiVixf/sMP
Pzx58uQZYHP40KE5s2a9WLOW1RhmMZqspjC72RJusRbaX85g4MBgBGEcwapX
qfrqxInffP31UyLn0P8O9ejS1Wwwwv9Y4N+90PLdCEtUENq1afvF51/kIzlp
aWmTJkywGIyFUvN3MEAIbFD8wMuXL+cdnl9TUl6u38CR5tgtVpvZYgkzm8NM
ZrLNhVmeocF/B/BHWG2qzw974Cs84w/zJzErPSaOKAKP9kKNmj/99FNe4Pnm
628qREbp/i9moykgILCsf0CY0RRls1ewh5dDC1eaPUJp4cr+M7IqUeUqR5WD
uNFOmZctzFzOZq8UEZnr97RpOtgXzc71tXvsaOWljmpP+fww+j7sg0n/u/RR
y9vDw83W0JDQMgGBwSEhcGR0hQh+X/vf2e8aPHv37tUlxxBqAGyiI6OGte+0
bfLUH1YnXN259+6779/e9y6xPe/c3r3v9p79t3ftJbZzN1rqWztvv7UzdQfY
26Jtfyt121upW3ekbtmuY5u3ibYJO9vFziZu/6atqRu3OLdbG7ekb3vr9vrN
DSqUdytSxFvZ3NzcGpSv8GjL9jvrNqaup7Z2g9hhD8GSN6QmrU9NZkZ3wh6w
xHWpiWuJQT8hOTUhidpasl2VmLomKXV1IrGV2Kc7VySg3VqxhnTYnuVrbi1f
k7oyAba3lq2Wje6/tWzVraUrxD2ks+rWctphO5UvIe+2YjX5ePCBVyeTz7Aq
iX3a24nrTi9dfmDq9CX9BnSq1zDMaCwbGGjRUIQB9uqVq3ILzxeff66FxxIW
VsY/oG616htenXL9nXeFf/9H+Ppb4f/+LRz4LOvjf2V99Amxjw9kffixbO//
E+3Ju/8Qbf/7or3zHrG9+8Gy9r0L9mTPO7yJe3btwyeQzq69ZA+8ZM9+8nDn
XtF2KY3s3EPsrd3CnneF9z7sXqceoOKpaUCUr7f32RUrBXjbHbvh+U/e2vXk
7d3MMre/Ldu2tzK3gm3P3KbcuWUHMfjT5u2Zm7YR27yD9DdsIduNW0XbBNst
ZOf6zbJt2Czt2ZS5jrO1G2XDPckbMpPWky3tPAZLWEf2sJ3M8CXwhuvpm5PP
s530YSd00LZsE7a/Lex+R9j/D9geW75qXOeuFlNYQGCQLkJbt2zNOTwpKSlR
9ghFnACyExJqMhgXDhry4L0PhS//I3x04NE//vnwvQ+IvfsPsIx972bs3S9u
qaXv3pe+ay9axlu7M97alf72bmp7JNudsWMn20/6zLaDvU1s29vYSd/6VvrW
HdLOt0BVyJ80Bs8Rbcv2h9veEt55b0zrtgiPl16DPyX1jwd+Hmzelo62cats
6zenb9gsb9HWbSK2ge3cJO5ZtzF9LbXkDdTWk23iOtmS1vMPHySsfbA68cGa
5HTorEmWLInrJz9YnUSeA9tVicRWJ4od9pDtWZlAbFWi+CbwkoS16QnwDgnk
Y2zYkr6Wfir4eOTDb0kHZd60NQOOEoC0F35lHxxftSam8SulAwJUQgQIQZT7
3Xff5QSejIyMZo2bhCvFJzAwqGq58t8sXS58/mXW+x+KnIDteYcaBQY5ge3O
PYAEse07ZSPDjYYDLT6kA71DfAh40HEnBuO4aSsx7OBOMNzJ22a+T59Mhp4c
HGHP/uR+A4AQdwfwID/NK1cRduzKkDHYRA41M0IF7SAPaykSMDQAAxo+REsk
RgcdjI7+qgTJpLHmd65Y82DlGrGD/ZVSn7dlq+T+8tXiw5XcX9FUz8F3XrUG
/l+CDaAOn5Z8yHXyV9soHls4/kSL3vvwzfhBIcEhZpNJFQu9UKPGjRs3suVn
6eLFfLYVQeFpVLPWxc1bwU9lvPOeCM+edwgnu/fxRvbs4LFB6dhJwGD8MEJ0
DQCAn8aGLSIMPEX8Q4RE+hGJL9m4VexvJA+FnXu/nDqjiLs7OClH8ECDJxTz
8U1ZtESAl4vMSMAwQnRR4YxoCJUR8aHIT5KSH9SHBJmWFWvUD1esEWUEAFi6
kjAAHYQBO0tWEMM/geHDxcuJQYc9GZ/P3pDSm560jnw1hlAy5QeggoOGwr5j
V+ae/cJH/9r96pTQUINZmXRDRjZ+7Djn8Fy9clWV5EKIXqNCxd8Bng8+IZAA
NlRhZJFR6YzkX6grEcEmYHBuRYGBrDDbiPF/gj48GTlBZ0Fsi9rWbyGKsV76
ExUQYcv2G6sTTQGBIC+6msPvh/7avv0E+MBJ1MWI22yYEU10MQqDncLaDRng
O1ZK2KDxoiHqxmpRLvihRwNIEA+tAS2LlqlN9Rx4OUMI/4uVCRShDWSbuE50
ZHjoqAqRUYPIYdde4eN/7ZgwMTAo2Ma5IeLFwsz/+9//nPAzc/p0PmyGgMpo
MP538VLhw09EbCBKeYvGKtt3iuRI2qIvJqzDRxf86DPR0OLBQguJCse2UXQ6
tPN47UZh8/b21Wto4XF3J2cZxMXFjRw5kv2VuLDoysLWtzIcoUJDEYZKOtfn
dCYRxeTh6kRh09Y3O3c5NmP2E3jaitUK58LrA0KC0qFiA3fqcvLmUmLa/SqD
1zKZQkOG1ySlr91EfDGvQngYkaLtOx/t3CP88+PXYnpBuqSSoAH9+juC586d
OyrxKRsQuLBfPCiPRI7GN6lo4VUFOdm0VVSG9Vz8uZ7nZ4v8+VW2doP6T2Ls
Sv2L+BwarCZJkQkNXIW3dy/v2VsbMyM8I0aMgC977Ngxcv6Jhwe6sKI+PhcX
LhHWbVaSI3klkR+Ok5UJSsck/swzVqwRNmxZ1KUrOcFl7AQhab2+pEAH+1rp
YMyo4GHYYIc3FVTQYUyy/4hpEXTgu6zdRKP3JJkiHBoYDurLssDXvLWrYbUa
kDfxEgR28uRJXX52bN/BRz6gPC9FV34Ab7Vzr+SSuBhGRcumrTqehTkUWUA2
igEGDj0fporZwQaRDQLGeodPQGCSNSFKwlph07afZs7x9PRQhT0Iz4IFC/DL
PnnyxG638xK0qmdvYcsOpapI4S50VkqBrhIY3gg86zYv7twV/eOe+MGEH9QZ
rQ/Suh4GjJYQpd1fuOT+G4vBHixcQkyXKAYhvi2vRSvWiPE/IoS/EXjIfBl1
HMK+9w5MnxkUHKJwSUbTmwsX6vLTtXMXlfisHzZK2P8BgQeBYREsC3Gxz2IP
ltuqZIQAo6FFZUlcUpMswqATwUqciD8cFp/Qfua6TU+SN1QzW1WeC+GZP38+
/32HDBnC89OwXHlh/aaM1VReVHHvKil6EZNlTdC7fHXG8tXC+i0iPB7kxLrV
3XoISRtkWthQOqJIFxXKiUOb/yYx7C9YRAz7lCsCmMrTsdgbPjNgA3hTR5xO
+2KOKcVFDzduEXbtbVenXggnQaAwdWq/qF3sAWk777wg9q4cGXV97QbhrV2i
b9qopy0IDPMmjiBJWi8LCOKBH9UJGypz/lfJIIaZ0bY98VyagHn48OGqr/zB
Bx8wHwcuzMPT8/SceULSOp3kmkdIz9IpPCu79YA3hLfC/3FGi5ZC4no1JCyw
UaECw41KImmLM2B07fWF9+e9qfsqWaMUAfYK8o3QI0OCj79B/lDTSGDnyNFl
uaIi0SKz5cyZM6qD+d233/LOKzA4ZGCzlgKEPSySUTGjrZM4IceRjCSuk/WT
S37Fb0H/ij8TRo4YwfKJj1R/E9Zv/t/0me4eHjiCPDxt27bVjffKli3LS9BS
UIyN2+S0epVDYPhcKX3ZKmHtph1x/YjySE4TukPqNxDWbtTRGaXUiHLBg5Qr
ZpjNmS92YD9q0bw35IcIEvvfmR5iJL9SKk/hsZV+sxDL/bZoWcXwcDNXUTQb
jHv37lUdzA3r19u55/gHBW8ZMkzYtpNLcCTDuCWZi0acEMLrA9ZdxYxGDEqp
s0jUSYGxJKuKRphbUT8/8SFNmetFRqo8Fzy0Wq1paWm6Lhu44vmpGxEpJKx/
CEeS5wRDUFUYLEXC6UtXCskbdvRVwIPv1qV6DQHYRp/FB7pICA4x73G0/Mxf
RCRl7gKCAW55m0uZ0Rr+FeCBl8BD6DDeqEdT+zUWXROQ1rDDK0r62o3tX6wT
HGqQXZjRNGfWbNWRnDNzNguT7BZrcEjod7PmCJt3OBMWNHyYsA6zWoUxxcCE
V0xhEnWBcWZMDbAvRrZcXWVlgrBha1Kv3irPVaRIEdjz3//+VxceaGvWrGH8
FIGgxd392LRZQuJakRCOE9H4HGrx8vQlK3ThQX4aRZXPgqAaBohFuTwkjiSF
EQUdZEbFBlLBbPY8Yto+PA0MHsIWISSdNxRaxChCr4o/EywcrRQpAn4mt20P
/ogPgbRZ/LgxYxg/ljBzpM1+auEiYdNWOWjhAxh+EocXB0UHHFOS6GXEgkmi
IiKVn5+ofLnGWL68ms7y4E4uGhES1l57Y0lAiZK8+JDpUS7h0m0pKSkQWhfh
nM78dh3AGemX7FDtmfIsXi4krtOFB9+qmiksY9HSDBYDw8Axz4L9eUqTtWUB
sblKDBAP3AOdWa/LzPB93thLmCFL85BV8jEeoCJh9IVahDiJirQKUoDEPn3L
BgXz/HRs1151JOP79WdzXmajqVq5cpeWrHiyfpOYFgEAietYJUQx1quklITX
Cjbuq6QIbRW3Z6UklTjds5Kr22vzYngmxiF8NKKcJwLxGfpyY63nql69uhN4
sMFzeBf2gtUmgGioZIfV9KSZAhGe2DhdePCtwvz978xf+IjxM1+ChDkU2RMt
kDtMXhgDjB/gBFGBhzPmkP7MuaQP21nzqL0uw4N/ZS/h8RN9nBRyM0O/hiIp
ZYvCyoT1feJ4fmymsKaNm6gO44C4/lzyZaoSVe7iwiWZkIzIU35JLMRSVFxl
bKT4RBzfNTIh8swOFvC5Giz7q2oGkC/y42+BPZMvhUHik7T+p8nTSNrDhc3o
uQ4ePJgtP+PHj+ddWBEP9yOTpwrwRbT8SCFuxpvLhDVrt/Xp6wgefKuivr43
5i54vHi5LD4EoTeo0T7Sgh6KkaPSEAQAYUDDh9PnEITg4Qxq02YTIzvpQ/LM
18kTZtA9/Fuxd2ZhFd9hDm6e6EmFpSvW9eqTO37CIHkHfhZnQiTAg8GEhXmc
larJHWWSy88Layd3xKB0tT4//JQQmxlkc4jSy0EoQAdaRUdrxUebsOu2L7/8
kq9UQ39e23bwnrLaKMt64I+E1clLOnZyAg80nPE/O2Va1uJlHDxvyirEVIXX
HBQZxglsAQmGCqNlxhxx//Q5916bCeTcmzoLjDwkndkiTsymz6avnUOeCQ9n
KkFSeUnoIOdkz3xh0bJ1PXrniR+UmpVrNJagHncc35zwwxv7kzZqZX3Vn6T5
HSFx/YdDhpMVGnQmgjFQunTpnCw2gHbv3r3g4GDehdW0WAUgU6+gBzsh1lrS
oROr8zjhByToxzHjBfBfoua8IQ4T/t75EIWJjEpqOE5wzz0EgErNvakzAZ57
r81AeDh+6E5i0hOmTMe/EkPAUJfEd35d/QHgU6F7nTlXWLB4XbeYsiG54sdc
OTLq4oI3MxOSpbpZgloW+PSW8cOPMjMVGNpcWPUzZ2VSLtPRiWaXrHi4bJWw
KrFeeLhWfFSlZuetffv2Mj8eHp5eHidemy6AMCrheQQxT8LaxR066sKD4Tp7
6EEfHhg4hPDDnBQf0/I+hfdN6Hc0/CA5BA+kgkECHeSH7QdaiFFsEJ7JxEQH
B28iPnMWytE9pHG63BfDqgUgkvOFeW+u69LdFX7mv5kJysM7DjZlvJxzOipC
+GyF1VpVD/nn8FmkqkjLnszPEHHvAF7m7bgBqnlSeBgQEHDnzp2c87N+/XrV
co5lHTuTEIiD5/GSlbBnctOmuvDg/EiNGjVU/OyP7SdAaoPBBgs/RGZel0MU
xg8yg0aZEQed+ikcdBEMZIOJDDx8dRox1gGbPE3mZwp7Mv/ymQqTIAR/R+iC
j/f6QmHBorWdu5XlpjByxE9E1MV5Cwk/WnfDHAq/fomfreOVRPUnvnSvO+mj
2snoYlVcqZYLavBk6cqqJlMexQfauXPngEA+i68fHgFZWLo0Wfl40XJ4OK5R
Y+oo9eGZMmXKyZMnGcye9H3WdeoqvLmMY2OurCeSx5G1Zdos1AQxnhEHeoY0
rDMoBqKYEENIJk0VbcIUsoU9E18jfdgykHiWyHaGTJQoVtI7i2jNFD/AtNmu
+6/X38gEz6Ust+pIh2rcddei6M4jS8VY1TQQDpm4X/c96ROElYlv9YmjBUOF
+AQGBuZKfLBVrVpVdmFFivj5+v46beaTxcvuLlgEATDEkH1r1tZdB4uJHq4J
OX/+vIqf5W07wGvlMJgzkR9Gixy0SIZD+SrlBIcbtkgIGgKj4gewQX7QoI9/
xc7kaWr88M3xf0Hk2P9F/zthxty1XXv451Z/gJ858zMBHl5MVGsDNNPEPEhi
hRNngaXJQbF0Js0OKxYhSMbv1O2ApS9c8ujNpVWMOuIzffr03MIDbeLEiSoX
tql7DKSuwqKl6Qve7Fq1uhN45s2bh2/C64/4YZo0lfmZocOPRI4Uz0yZoaYI
FYaNOKMFOeEfjp9MDJjBDm8IEm55ulRPYB32nuNeFSZOW9uuY675Af81e14m
yI4WGKYbrCbPDzq3kEBRpceqAj/jo2vixB+dR16wWHwhLlHg1ioIKxP2aiIf
GE1fX9+LFy+6wM+//vUv1dC3r1RZWJF4Z9b8JhFR2gl9Bg/vKy9cuODh4cHK
UPDXcfXrCwuXSvxI/kvWHArPVCn8mMw8iOS5GDAoDjwwDCE27uNevTd2krzV
GqNlzERi0tPu8g9xy72hMGlacpsO/qF54IebtZHn/rBiiR1VWX6+VB6f96Zc
98CJYMWfFqnnEIktEosP7L9gM8gSh4CosHglhCha8YmNjXUBHoGe4+/v78+7
MGPpMsfHTaoVZtYugvWSVlCrAq1r166VKlWKLwX0q1FTeH3hg2kSM7DlZWeq
FNWwmETlWRgnTBYYM0xwwHDEERIAgPEzZiKyAdu7oycQSGA7esJdye7RneSv
I8fdHTWe9OkWn4l9YdLUte06uKA/F2bMfvwmq33haL4hLglghmMtl1Xf4IBR
lsexz3biln8hK8yyGWf2f4n/tVh/E5Ys/xxrPpz4YBD7/fffu8YPtNatW7Oh
h/f19vYuW6y4E3g2bNigeoerV6+WLFmS56dnlarCnAX35eRaSrQnc+kSMsO8
FY8NMsPDw3slST3u8tKB/CAVlAfZABI01cOR8JDbOULaP3zs3RFjhXGvJrdu
l3v9ibzw2szH85dw4/imGh5WDZvHleL5/VrTzvJoJ5T5yT5VdX3uggfzgJ8V
bSvpFJxr1arlMjzQEhMTFdOvtBbkCJ6NGzdq30HLT7OIqCczX39ASi5S+swn
4NpkStdJsegFmEE8OJERxYQ6IDUzo1WcABtj04aPkfAYkzZsDGzvDif70chf
KTbwpzTyhNHCmInJLdv6c+s3csrP1JmPFyxRrjnhSFBVv9mUinYi2NEaA9VL
+Fdp1ydIO4U3Fh8dM4FMdnHig7W7zZs354WfU6dO8XPxug3h2bRpk+47AD8l
SpTg+WkSHpk1e366WCvmKjDosJjP4gNjFTy84PDwMFqooyGjz+vMCESCaosE
D/JAbPgYuU8NmEkbNpb0h45CuztkJG6FUeOSm7d2lZ9FMjBaKlSlVDZ9oyqU
qaYCVfODOfyrZBCODq9TVys+pUuXvn37dl74gVahQgVdh8X+FwDsww8/dPRy
iH/KlCnD81M5JDRj+tx0rP7xmsNXZhAePjNifUfMqMgZPhZFQ8JG2iMpDBGT
YWN4PBgkdwePAMM/YV80+NOg4XcHDhOGjElu1soVfqbMeAzxiaO5YNV+spxg
nmJemJ8HZFOBrK+a7mFTPFr28D2pPZk9/8qkqWWLF9cu1ho4cGAe4YHGnxSm
hQek6aOPPnLy8gcPHthsNgU/wSHpU2enE5+FIoOmLNrw7onFwFIkIwa3XBgs
YoNhjCg11DERJRmjtNEiHkNHUhtFkFDZwGF344fJHWbwwgFDwVzn59Xpj19/
Q5rzVc7IzOT2TJ+tLqjS5FRbMRNfgmX56cqZwRlzNXvmiOsQpkszfTPmCguX
rGzTXjXEHvRkh6/z48J9/Ip6FTxFixb95JNPnL8c+FGcE1TEze4fcH/KjHTw
U6o0ipHD6jB8oo3Y8KjwzMiaI8YqYqxLfNBoohsqAxJkWoYrIAEDSPoP0TH4
E+0Ig0YmN22Za37CIy9MmPIYfv7TpUl/biLvvjQLzBXBZvEFeWV9bJbMj1QA
kSfv4Ani6gIFQvd4CClFGTNfz5w9v7pezbBKlSp5h0egK+r5BJy9P0Q1ObkS
V3p6ejg3mQvhd8miRW+Pn/KQFYf5mjCtzqmwUfgplgTxeAxHfzSaoUI6IDXg
jxg8vLwwT4RGqBiqi01av0G83e03mHTiBgnxQ5JeaeGK/oyf/Gj6XC0hcgTI
rRxQoyKNvr4QcfywrWJuiCOTPV94/c1P+8XD6Hh4earGd9GiRfnCD7SWLVvy
/IDPCgoKcn7SN2t3794NCwvj+Snt55c2ccpDnHdgTgoMWeIzbi7vVvMjmcTP
WDGYYRQhG0xwUGcGDpMRcsBPGoXkbv/BWn7S+g4k1meA0G9wUuNm/gaX+JnB
+NHMzjhEaCYryIv80JlBcdnA1JnS+gF+4YFyHQJDlHvCfeBnweJYzSnt+PC3
337LL36WL1+umsjo27dvDl975coVRf7u4VGqqN8fYyY9RP/FuyrcKmNjkZ9R
E5iTShOZEeERE6XhY8T8CINeBga6qoFKP0VjGNKBPdjvR2i5OwA0Z7CIShw1
oAWxiR1AjMKT1quf0HdgUqOm/sZc83N+/CSZH746qpqj0a1mYEFMXIsyQ547
niJ15ClCB1jiO0t0Zc58/dKEyaX8/Nzc1ZFz69at8wseaCdOnMBQmb1/+fLl
c3htbXX9x8PDx9vr5OChWfCV+ckmVUqF1RtWKx6BhTsSFTOdEaMdKadWBDYs
kkHNIWwMRVNKCvqjeEoI1RbsAzlASx9qEjPEevdP6xWX1rOvEDsg6eVXcs9P
xPkxEx5Nny0OPcsXFEsCpssTfMwmc8sA8E9TNO/AmGHrCnSNQ1GYuyChVTvV
PBSWffbt25eP/AjKLB6D85SUFFf58T45eJjID5ui0vLDQmXYjkC1oZW9keNE
P0XDGwU8YKpImCA0TIpnBivgAVTiaAc5ATbAgBbsgOHOnnHiQ+gAQj375oGf
yPOjxj3SVrdUa054MNgerKOqiOLfQfW2rB7CpoG4VXNgD6bOFGbMrWu2aJ1X
SEhIRkZG/vIzduxYeSKDIrpjx4488DOc8KOaX+CxARsplfvEio3ED60Dy2qD
wTBxUsNEP6VFyBE/GM/EDhQRYiARTuKIxcSm9YglzMC2e5+0mL7EuscKPeOS
GjT2Nxpd4Qcddw4Nf2IIA/Zz+ELG0uTpaqNCJMyce2jICDdycoSHih8Y6/yF
B9qBAwdUc/E5XIqvnj8l/PicGjQsC74azw/LzUeMkzRnHFfxGy1rDrHRYmys
SMOHiVGNmhyMh5WxjUjOAAU5THCoyCjg6dYb7U7XXmldewkxfZPqN/I3mlzk
h18uojWc6Ed4MAnVfQ4+TbuHn+5R9ZlMTZkhzF4wvWEjlfjg8okjR47kOz/3
7t1TlZEbNmyYkxeePXvWTbqmkBddQu/h6fl9bH9h0jQ5POa9FcY5dCpKLONQ
kFitWE6m+ASKr9twmiN6KDEejpfJQSNRTZy4BU5IX9IcrQE8XXqiCT37JdV3
SX9GjHkEg8gyBX4BCfPmjBnd1Sa6+1VP4I0VRpBJdF5TZmRMnl5OcyU6eNig
QYN8hwdbly5deH5Kly4NUGX7KtX6MbIE2t39sx69RX5U8HBTD1g6lvVHFSRj
Js6nVDTj5qp8g+UECix2oJhA8ZqDUoNRDRCC7gldFagNbCXlYeTc6QwWI3SP
Tarnkv4MG/VYVVHnK126+3Wfo13C5Igf1Tpe6tSEqbP+r2dftyLq5X85D0tc
aBs3bmQkYAj9ww8/ZPuq06dPa/n5vEcfAX4I0hob9doJPbcluiqy5XwWV/HD
jFuu27CUiuVQxD2xCEdyUqKr6quQGuQHrGtvAgyS0ymG9GHbKUbo2tt1fmAo
cWUaDwz9KenULriwENcgiX32cm7NmzMVUi6tFGbOG/XCC88mcmbt4sWLqhX1
69aty/ZV3333nQ4/3XoJ46dIyyekejJXGFQFPHKoDKacaNCJh1mfhTR8Ao7w
ICcxfeXYmAlO9z6izpBtDAWmB9l26EasYw/YCp1ikurUzzU/4ZHnh458DF9c
XF7CqS6biOGlmJ+sYcbWubEqB8MMIXTi3eA5414Vpsw8ET+0tJ+f9pI+U6dO
fTrsiK1evXq8Cxs6dGi2L/nkk090+OkaI4x9lSzFGSkVdpQlZdlhMWwGaQIe
vSkGViJW51O94qSUSgJGNBISqw2xYfx07E7Iad+VmdCpe9JL9Vzg59fBwx+N
mSRN8krLA0ZqDH9QbNnAiLE6z6HwyIUyaW3kXalcr5r6QaUSJk29NnJc+YAg
beTsla81Z902d+5cnp/GjRtn+xKH/IybLK6swNhYtYJCNdfJ5sEpPGks1GH8
MPFhpRs0ICcGA5tYJTbECCooNaAwICydeohS00mSHVFzusvwtOtyp01noUNX
F/kZOOzRyPH8j0XBzwhuPz9N44gfUuVQLqHkCyBKA34eTpiSOX5yI4tVu6AC
9sTHxz8dauT2888/s2QKQ+i7d+86fwlGTexzcvy8KgvO0NGKiSq+pIzKg3Ey
V0NWKA+fjKOfYtazL8ue+BycpOHYYbENQIL8MD+FtHCyc6dtZ2KtOwntXeGn
SnhEyoDBD7F+JWaUYyTJHSNXRDWm4E1Bl/QOasDGq/eMGn9/9ATh1WmDqlXX
woPrnI8fP/7UwBFbVlZWxYoVeQkqV67cV1995eQlqvNYRX669BDGUH4k5RHn
zVWLuMRJz+FcDXCIDjkKP9VPpKhnXxkepjkkJJbcE82kqOxQqQF+eD9FdUbk
hzJDDDptSEdo2zmpdl1/U274MVN++g16yFXOxS87mH7ZIVIhVDUjww4Lx5IS
sDFs4Yq4wAkXsbDwkkqcMHFqwivN3fROuYKdXbt2fZrgyO3VV19VzaVCmzZt
mqPnL1682AE/k/isXD5EbPYTp67ihytqOyI/gxV1YzbXoJIdFhVTbNJ4teks
dfjwBpUH4UFm2oiCc6dVR2LQadkeOlmtOibVeinX/NgjUuLiH/LSymcE/KoA
+ld+RQqPFltJq5GpMQp+ho+ROmOFcVO+6967iLv6MpgY+UB0AWnyUwZHbHiN
cdVyDnhYt25d7QVIoUFIr+Xns87dhDETFdNY0rJA+Rjyc+UDWCV5sKw8bNKK
GdZzWBkHHRZ0xDgnRg5vMBPvTI0xw7yVpDOi5lB+brdoR6w5Mdf56TuA8DNw
uNqwfj6QW6GEW97Yn6RZG9XKWy1IqFdPRk+8OXR0RBl/refCqajRo0c/E3bE
hiGNtnrg5+e3fft21ZP5S1HJ/HTsIoyewIsP0XDtUZVlRyInTirsxHLT4n0o
PGRmqo+Yg/MxDw8PSE1nCZ4O3cXYmOcHIxyEBwQH1KZle8IMkNOsrWhN22S1
7JBUq44r/gv4GTSSBXLkd8HP88IexRHgiOJ38qvglPOAWpYekLONJneJKu8o
7OnevfvTq/k4aps3b9ZFCNqoUaP4Z/bu3Vvh7zw8vL28jvbplwmumZ/A4sJj
eX0O2Tnkbr+BiiQrdoDaW4nTmlLRTxvtADAY3shJVg851FHw00WUHeqwJM1p
K/PTtM3tJq2ymrdLqpF7/QF+evd7CB6532BpxZFy3aPO1x8qL1IaOEzMQ5lk
ibrEzR1L6sRAEkZPSmjcVLsCGeGZMGHCM6RG0f75z39iFVr7qcCXsfsU9+rV
S8WPj7f3id79MsE1M1keqISHCo54PPsPTOs/kOhP3wFynsVKOljVUUXIkuzI
oXJHKTzu2E3OqgAbFBzcguYQ2ekshjoIT3POgBywxi3Bspq1TapRO5f8WKrY
w5EfcTUs/YJpNJyjAivOvFClHSxlmrSDyyNZyZ1f2sQqG+whB5IwfOyJXnHF
fLx171tRgPBg++ijj7QIoUs1Go2HDx+G5zRv3lzLz7FecZnDRstBsnIFOzmA
/TnNIb9WDJV5t8XNksfE8tNVXA2whxIe6qrQQyE2bWiEjNi0FgOe20BOyw63
W0o+C7GhskMM+XmldVKNF/y5a8vnmJ+4hwPgC8ZzZXP8jjj5ImWXcfGiyyZz
vvG8TJGjoYgMObGKl1YgUJDSBw3PGjK6nlF9sjkOEMQVBYGMun3yySf86YG8
LytatOiXX37Zrl07FT++RH84fuKHsVAnTVxEOgSPmzyHFctFy7g4J4ab7uRS
LZEcVjfGbUcu1GH8oOYwtSHMUEOHxXwWMPNKa7Jt1ILC00Lkp7oL/ESc69k3
I06ayWVr2Fjxk+wcLM72xnFLTfrJLIk/qAHcOn8VPwPEFQjCiPFv1mnopnff
Coh5CoQW3Xbw4EF+hRj/Ob29vf39/flrwOL655vxQzLYlCjAg/oMh0JU8sFy
baevkp+ecaLyEKlRRMuKYqBKdkhKRWMbERvmrUiELDKDUoPYoOCgzwJsmrS8
3aj57ZebkT7dZjVqkVS1liv8xMRm4HcBhFTfkRkQgnUJRIjEe/3FWWD5OfKK
JlmdmPcfMFQYOvpI995Fvb20a5srVar07ANm5w1cFcSHWoSK0Kb4/JSfWwOG
ZgyVzpJg8aF6SoI7vEx8xAydqwpKSbrMT+eesuxgtMPScLEG2FnMrfgguVkb
ojPNJH6gjz4LyGnYTLQGr9xu0BQ6T+q/kli1pgv+61yP2Ax+ei6Wq2L1HSgv
0ceVtKi9vajkxg5QY6aa+OMWdd8DfgaPelnjueChj4/PiRMnCgQS5+3XX3+N
iFBfPUbbIJALK1nqzpAR6VjwUdYGRaFmFR4860E1K8GvtcC5cpzrZNOdbD4C
EyuxEthJLAAyhwXygg6LaQ64J/RWosNqLhrCU/8VsNS6jW/Xa/Kk3iuJVWr6
h+Wen26gP/Fy/tiH+3aYF8RK5dDYgfKagT4aeJhSsV8ZO2EkbpAwdGRywya6
C+O1F0j587Tr16/XqKFzf0wVP5UDg9KHjnqAa91Z0sovTlb5LHndhXJKC8SH
TYCqqjpY6mHFQJaSQ3iMaiMGOVKQ3FwKdWh4TDstZNmpT2QntV4Twk+dl1Nf
akj0p0oNl/jpndELq51c/sjWQLLfiBjm0QSBVddjpcIXW9Sk9GiI0+OBQy/2
jivrV0zruVq1alUgYOS83bt3r1mzZtpqA/8t6hpMwvAxD0jYw5a1Dxb50Y15
2PEU15dypR7gR6wnY8DTQzFXzs9EcAiRmIdRBIaC80obUXa0/AA8gA1VHtgS
fuo1SaxcPdf8hIef69wzI6avIvIHX4xfiixGwqRSubatV5yi2MU0mdXB2NJK
yNRAfIaMGFChotZz+fn5Pe3lGfnSMjMze/Qg94xz17uWuLunp6+X19bGzSHA
u9dvsCKHjdObD2UrvmJidQrLmGqBBKmiZZXy8PzQyEcUn+ZUhfj0qgnNsEic
3JyEOtRnEX5eaojkiPrzUuPE6NzzYws/1ykmA5WTfRcCEvewh7RoX21xCmni
ieLcnDBw2JdtOrjpXcln2bJlBcKDa23MmDH8KYeK3wItXm1p9IowbNQ95rb4
MLKvRnlUcxMY9oieS5qbUC7xYmstGDkKzWFBsiraadiUYIPwoElhD4EH7EVi
T2q/nFipmiv+q2OPjB6xiiI5rTmI83Rswk7UKKkjihKVKbYQTiRH7j/o3T8z
buALwaFa8YmOji4QDPLS3njjDe0ch4xQEbfFdRoIQ0Y+wDII4ydWqjCzdaf4
A2T8sHVfxNi6nRjF0gtWUqaFHTU8zdrKrgoM1AbhAWyoh0LNIbJTvwmEPamS
20J4Ul+o7zo/7bukd5Pgxzon7ZNqOV88Z+VQ5uOQJezzi29jYhldQv+hyXUb
qA44FngPHDhQIAzksW3ZssUhQvR7TahaQxgw7FHcIDml5bMt5rliYjXKgzFP
d4dui5sDvd2Cqwo2VcIDxsU5hByIk+tJ2FBvRbYvSvDUbpAnftp2Tu/SS6mc
MXL+SHBiP42e4i8F0OJqpPAEqdLeS8SMKlVGr7ibMbGG4iW0l4Fq3rx5gYx+
vjQgv3hx/UtuulO/3M0eAcKb1W/wnT7x6lXuPZUVZnnFaYy8dIdVlXFWq00n
eekFK+80Q3LacNi0wEqyKD4NxPScuCqmNig4/JaKD+GnVoPEilXLml3ih03m
dpJi/s49FWd5MH7Y4gGKlmI5Ad3KFbDufYS+g6dWUa8tzPsFVP8M7ciRIxaL
+jxrMbSjP5A6waEXu8cK8cO4GQpJnNG/8z6rs2Z9Msuz2nVRBzystgzGBAfs
5WbEW2FVWart3EbBQWPAgNWqh7KTWrMu6des+6RG3cQKLvBjP9emc3qnHvK8
P6+fSBRLJ+U1/D3l/bjsVkVUt96ZPeNOt+9W3MfXTXNKRf5eSaOg2tWrV198
8UVHeT3sN5co+e/W7cGX3Y2NF6fU+YRLKztY6mFxsl6qJdd5mvHi00LSnKZM
c2S3BcrDw0OwaYDMEKteh2xr1HGVn/Bzrdqna5erMRNXmHDraVVcqUyiSOgz
IJ5e0f35Ex/WHj161K1bN0d5Pfnunh4b678MQWAGhEA9FDMUHDl6k+l8bq4b
KvO1wcYtRM3hcytkRkrPRbVh2CA5zKq9mFm1dmKFyq7w07JdOoOHLVdj60nw
S+HCEpmo7mqueJnq0jMrJu7HFm3JbSI1J5Pq3qL9L90mTZrkLClzcxtdsRKE
glk9+4nwsDwdl36pKoRah0VNDnvkVItLsjh4bvNBMkuykB80FTzUnlR/yRV+
bOHnmrdJx/CsTSfFShJ+6SwzhS51x1MXtVAJMXExVrub3iKNb775pkBG+ak2
PCNDF6Ei9Fs3CAm90LGb0Kt/muz6lbKDxxkPu674NJeUB6wxnT1vRN2WMs+S
ZYdFyAAMwFNb8lk1ZM0Rt9Qyq76QUC66rNnsOj9YCWdL9NtIHV1TgYQdeliy
uvb+d+Pmbu5FtGeyv/TSSwUyvs+gffbZZ2XLlnUSUYf4FfuowStCTL/7IkI9
FOUd1ayWPCXaVtYcJIcv72A9kCIk5+agOWB8eq51W4gN6bx0q3ItsMzKNROi
XOKnWev01mJgL5/ToWs8P0ydmNej/i6tY3ehe2wbY5j2SLo9hWuI/alaSkpK
lSpVHEbURUic9HqVGk+6xz7u2ltRW+antBwFPCzPQs0hi3aay7KDzDB76WXZ
W/HwID+S5tyqWvtWlVq3Kta4ValmZvQLCZGVXODn7CutHtAVRzL2yp+AYp6O
GXN2begXl35BWZ1j/t2ouVsRHfGx2WyPHz8ukJF9Zu3+/ftdu3Z1NM2BvqyN
yXypbSehS2+ZHEW2xcU5aGyVKa674BdgAD8MHua50DDOQYdVQ+G2CDNo0TWJ
AT8Va2RWrJUQUdEl/9VW1J/mUqiGOEmLkWSieBVqwy1eYvLbtrPQsUcbg/rS
zV4u3W7yWTaQjqNHjx45cuTw4cMnTpyA3Dwv7zZz5kxH4RD6MlOJ4h/VbwwI
3Wf8sLXKuvNZDB5QG34Nhqq8g6ZNtYCfai+JmsOwYQb8lK+WWb6aK/xY7eea
tUkHd9ymEymJN+ewb85WlYjBvyJAaiOt6mdC1LpTVvtuXzZs4uahzmbhx+jn
53flypW8DMrTa3hTOb5BJBMdHR0bG7t79+4c3h9c1cBT+/r6Olo4BPIE8eH0
ipUfd+qe2aE7NyshYdOCi5YJPy2Uiwabikk6Lzss2kFmWJ5VA/mh3qoyx0yF
6qg8AM+t8lUzy1dNCC9f1mLJBT8WaxWz5YS9fHrthkRtaKlcUWFoLi1Dai6r
E0sn2clod1qSTlqrjkL7bkR8iuiIT8+ePfMyxJ9++unvv/+el3dw0gYNGsQP
NOaJPEvwhGPHjuX2bUHQ8BKvuuEQ+rLGwcFnmrYROnRP42uDDBs51eKSdL7I
wxDiC8tgfJ5OlUcMdZCfSqLmUIqq3SpXGSyzXJUEe7lc8WOxWCtarJ8Gm1OC
zVes5e/UrHvnldZ0eredLES8IvGGbo4j6knrTv+t39jN010V+eBwQHriwshm
ZWW9/fbb4eHhS5cudeHlOWkQkvE3Q9HRCqnFxMTkdp3tvXv3Onfu7MiX4ZuX
8fXdVbOO0K7rA1yAirNaWOFp0lLmh1txSgyxYYVlkJ0XlXUeEvC8pAiVefFh
/JSvmhd+oi3Wf4Vafww2g50ItlwOi0ytVDOt3it3wJeRX0QH+RRFMBVCuMgW
5ahFO6F1pxiTWVd8IiMjgYRcHfnMzMwNGzaUK1fOLZ/uueOoqS4m5qjhGfHQ
Jk6cmJNrJPJt3rx5zhCiCz/iLfbU5u2Flh3kmAeTdF1+IOwRy4NSbRmnsZiB
w6r+EgiOyE/VF0R+KnHOi7othOdWVOXMKOAnd/4L+KlksX4eajkWYjkYYvku
xPJ9cNixINMFg+1mVNW02g3uwHchctRRXMnPzjvT8POodacjDZq6e3kW0buS
xuuvv56rA75z504kx+1pXjwT2+TJk7NdIc9/F2gREREQMuXqfzlw4EBAQIAj
UHHWvnzJUl+/1FBo0eEezqQTfmiezhV5RM+lKhKyCg9OZqHPqv4i5eclWuGp
SYo8lajmEHIoNrCNigZybkVUuhVeKTO8UqIt1/oD/HxB+fmJ2o+AUIj1h2Dz
0SBzSqj1ur3i7aovpjVodqdZG9GRoUcGaeVZat5WaNtliFXnVAU8YrpXsdBt
4OZwUhKbv7//U426wXmZTCZV8JxDisaNGwcimfP/67fffoPfgqPU3osG1R6e
HnMjyz9+pc0TnFtnhcG6jXG5u1gkfFHK0Ik1kGbS6zF+xGgHDDpEeWjOhZoD
23KS7ERGEwuvdCsiOjMi2gX/peLnUIjlcKgVDED6AfYEhf0SbP7NFHGzXNU7
NevdgV8Epvn8IskmLR82bXfu5WZ+Pt664tOoUaOcHF4IjyHGxqEB5HCm9eOP
P84FDblv169fHzVq1IwZMyZNmtSlS5eKFSti0uRklLGhO6tWrdrBgwdz9T9O
mTLFmS+jQtQoMOhkvcZCs3ZpdNEpiZDxRAk+WsYpCT5Vp1JDYh7qucQ8HTSH
j3kAHtQfUB7GT1Tl1HLRmeHRidbIfOHnSKj1KLUjFKQfqRydC7Ves1W8XblW
Wp1GdyCuA0Uiy97IIm2hZcdpEeW0xyTnp+ckJSXhpbz5m6qPHDkyV0OTL+3s
2bNr1659+eWXnVDEYiES/ZYp8+233+bqv3jvvffwy+r6Mk9aqS7p45NcoYrQ
uOVDyo8i4WIBMxopD8pTEqLgID8Q7ZAgp5qYqqPyEGCiZXIiKqXaKlw3R6Ya
bYtNNn+JDdf4AWPwgP0sGYJ0JMRyMth80Wi/EVX5dpUXbtd5+U7jlg9atL/2
SpsQcm6Oeg0DHKJixYr98ccfTg7mjRs32rdvr/pJQt9utz98+DDXw59/DbLv
AQMGeEku2ItLxDw8PCpXrjx48GAgAXh79OhRbt/80qVLTZs2dSZEHiSo7hZs
OP9iA6Fhszss5nlRsWiQKA/B5iVNnl5LzNNRcNBzoeDQaDk1Mvq2vcJNc9Ql
Y/g5g/VYqPVMiGWu0RaUf/wck+A5Qe0kNfjrkRDr8eCwMyHmS6bwG5GVhRca
rIqqBF9W+1uCg9OuXTsnh/E///mP0WhU/RJxdfSnn36a20F5Gu2XX37BFT7Q
SpYsCV8nOTn51KlT+fLmzvMyrFQHFfXbV7EqIPSAT9XZ3ASfoaPDqiwpDzIj
p1rECDbhlW5ayl8xRVww2k+F2mCUf6LZE/CzwGQNzBs/hxzzAwb/HdoJuv94
qPUsUBRqq+jr5+apFh90Xnv27HF09Hbt2oVBjpa6GjVqpKen58sY5UuD7Gn3
7t3Xrl3L93f++uuvIyMj3RysQPPC7N69SN8Q043a9QWIglB5MENnk6GQnlfm
5yMwTpYDntTy1W5HRt+0VrhsigRszoTa0Kcc4WKVlNBnx89pg+0MtWvG8A3+
wSDouuJTqlSptLQ03eP2/vvvO/rpgf4ULVo0MDCwbt26ixYtcqHw+9dqDx48
wAK4IyFyx1v0+hX7AISoXpP7LzQQAx6cFQV++MIy1pYrEXhSy1WF8OaGrcLV
sCiIOs7Rn/zPyu0xabjPPSt+fpHgOWuwXjPZmxQroRUfL6eXZElJSQFCnGTK
/AwCBKsA0qZNm+A4P/3BLLC2f//+kJCQ7ITIfUio6WbNOkKt+rchyapamyhP
FamwTMuDqaA2tKRzw1L+sin8PAwTCTyIyzhpwCBE9CAn8omf/wu1/OyAn2PK
+EelP5eN4R8HmSBn16YoCMDbb7+te6ych46qxpIdiJRmz579NJzIn6Rdv34d
fnFOjgyZMiviVr54iU/LVRZq1btXrbY4qx5dM7ViTYiKb9pJJvW70X7BYAO1
gWFiP3no/yI91PJzJA/+6/8MRMq0/LAUTOW8fjGIn+emKbxfybKOxMfPz89R
5jVx4sSIiAiMk3MIElMk8IkzZsy4f//+0x/PgmkQFqIQOSwzuheBgGFciCm1
YvWs8tVv2Stet5S/ao66bLRfNNhAcCCfOiP5iDMSOb9w/JykzuuE5F+O0opf
XuIfXf3h+TnO6Q9+kl+NtiOhllJe3m5e+mevOM+8oEEWs3bt2tatW+PF4nJV
+w0ICNi8efPTGsKCbjdu3IiPj89GiNyLlPct9nGgMd0YcdVo/5WOyHljOHRS
DPZz1M4a7AweXn9OSMOaX/zoxj88Pz8r4x+w68bwWWWC3DwcOGs3N2Ajh4fr
6tWr27dvB94YSI5iAB6hP0mC//QafEFc/uG4WO3u5ukxvFRZIOduWOQFA4l2
GD8AD4rPaU6FHPGTF//1ueP68zFOfzAEgu0vNHI+b7RVKAppu97KFnr1eBcu
zHL58uXk5GSIlr1oFuYIHqDrk08+yadR+lO3jIyMOXPm+Pj4OPpNFaGVRotP
0d2BRkAIXBjAw/Oj8mKMH95/4ShD/DzfZHWhfpgtP3wKhtE7RM7bAwy6aTsO
MTCQl+OWmJio+6PDWHr37t15efO/XDt79mxMTAwKkf7KfHBnnh79S5ZNMVpv
GiO0/JxWxj9sNBk/x54yP6oo+orR3qZ4ad3IGfmBRMnlw3XlyhW7XX3umJd0
7uqCBQvyNhp/1fb555/Xrl3bEUXuohD5bgoIgbzmkjEbflT+C+uHeeeHIOSY
H/zfz4favgoy+xDx1PktYFZ16NAhlw9U/fr1dcUHdvbt2zdvg/CXb5CdRUdH
u3F3f1YLkYdHj+KlYQRvmiJYIqZN3nFAj3GBrsv88Pm7Lj+q+uE1Y/i4Uv5O
IufIyMgnT564dnxAuHR/X7CzSpUqLsxUPpdt6dKljnwZClGAt09C2RAYqd+N
YvLFEOKd11Ep+cpffpgLU/EDdjbUeibUZvMtqpu240C7vNz08OHDunUP2Onr
65tfs5bPR1Pdw0VXiFoUL/lNqOWqKVzFjzZ5P0pG9mnxwyN0xRC+wT/EUeSM
Y/3++++7dkwg6tYeE6wc5rwa8DdpkN7Cb8rJIjcPKkR+Xl7zygb9ZiSxkJPg
5yiRBVf4ibZYPwu1HFXGP3wIrVrCAZFzi+KlnETOJUqUuH79ugsHZNOmTY48
V4cOHfLjkD9vTXXakbZ5UoRmlgm6Ygw//TT5OZYzflIM1n8Hmb1o2cERPzlc
rapqjx8/1r2clxtdgfb0zvz6Sze886+TWivA06F4yesmuyr4yUd+SP1Z8l+H
KDxsCfQR5fwX+LJLBvurpQIciQ8O98KFC104FMnJyY5yrhUrVuTHwX4+Gy7I
1x8LT0+zT1EYvovKmS++8sMj5LL+fBpqgTdBcrQpGPtfToEZrJE++jVnLylz
/+mnn3J7EB4+fKh7Bp8bva+Ky6nc36Gp7iTOWhHKz74g0w3quZzwI+tPiOX1
3K9fRX6OovKwWXiOH4bQBUP45oAQN09nkTP4IBdS7B07djgKm9977718OtLP
Z7tz507p0qV1fnoe7q+WDkg12U9rZt5PaJzXEepuzuaBnyP0zC/dEtBRaa3a
ZaO9YwmHkTPy06NHDxcOgm7BEPbUqlXL+QtV57Tm9hTX56AdOHDA29tbVUsE
eBoWK3HJaPvVYM0JP4fzxo8q/9INoeFjfBcSVtzLW2eVPDfikEPl9gicPHlS
GwSi+ODJX3fv3j127NiHH364Zs2a1157LS4urk2bNi+++GKFChX8/f0DuQYP
wQ8CdfXq1WvZsmW/fv2mTp0K4dOuXbu++uqrEydOwK81V2f8/cnbuXPntDe5
A7fl7+3zQ6j5N6N62uIkV4fhPdfR/ODnMOe/ECFefy4b7LNLBzkRnyJFisCv
4JdffsntQZgzZ45WfOCt/Pz82rVrFx0dDfkXf76Vyw2XVZtMJgCsbdu28fHx
QNeqVav27t37zTffpKSkAF0Fe8ZQrlpGRkblypVVh87di0ykbvE3XDOFs2U/
pwuIH76KeM5gr1m0mHPnVbFiRReOQ/Xq6guMM4TY0IM6OVrOkZMGagYvx+lX
Jw2IBfmqXbs26Bto1+TJk4Guffv2ffvtt+fPn//jjz/+VKeE4EpX9Sh4uI8u
5X/LFMEvG+P5Ycvmf1bCA/ZLiNkFfrTzp1p+zhqs7waa3PTWOfP8DB06NLcH
4cyZM24OpgKfTfOkzYM253SBp7Db7UBXq1atYmNjwZMCXfv37//xxx/BjwBd
z/L+m/Pnz3fT1FoBnrrFil8y2s9zC1aJceLzM7fyJ1/4Qf3B+PmwMgVj/EDm
Fe9gnbP84d3cIMzI7XFwVPb5kzRPqWVLF4ReEREREJW1aNGif//+06dPT0pK
gpjt4MGD8Bu5fv16PnrGjz76yE0zS+jmhWGP5QqdqvhFWnaoCn604nMkn/g5
KNUPVfwcJx2LwdfXUdnHCy+07uUFP8PcHoo+ffr8mfnJYXNOF+RHAQEBkZGR
EHcBXYMGDZoxY8a6deuArv/+97+nT5++du1azmtcZ8+e1cbMtNrjsT3A8Icp
nC1b1dUfxg+/cgMH3WV+PpX4+YnjhyF03hCe5B/qpOzjRfmpVq1abuGBhktZ
dN+T9yzZ/vxz0jDCx7fNV3yyac6Df19fX6ArPDy8atWqrVu3hhgAEgpIY//5
z39+//33oF23bt1ih+vRo0famBknuSbSag+/YOw0xw+LnFX8oPjgcOeFn6OU
n4N6VaDzRluL4sWzdV5jx47NLTwQM+DKXhjWbDOsUqVKGQwGyNlr1KhRv359
SKAgDoEYMt5B69GjBzwBRgR8CgyN0WhkF2bRbfTuiM+UKy/NhRa1DRJGoMti
sdSsWbNbt2516tRx04uZmxcvedVkT6HVnjN6C+bxhB2t+BzOJ36OUXJ4hFB8
ToTa/i/EXIzIYzYH4Z133sktP59//jk7UPA+wcHBqsx69+7d//73v48ePXrl
ypXU1NT79++7Vr3JysqC1968eRPE/4svvti8efOsWbNGjRoF+NWtWxdGB4YJ
s7Nnj5CTpqu6qufA7zrS1/eUwfobt05MN/Jhk5jHlJHPoXzl50dOfCAcSjHY
p5cOzFZ8QEYuX76c22E9cuTIvHnz9uzZAylM/kaYuWqPHz9OS0uDOAQkVDtA
ysHyoOYJ5u5V8KjBxyju5f1FcNh1Y7jqVAsnZ1v8rCc+lB/LPFM++C82kQpb
+E9rkLKPs/wajnn16tULZOjzt33zzTduDooJgIqvt3e9EqUiixYr4+Pt5+1N
rljoQa6MQc0dT8V6lmgVoaXCbQGGW6aIswarNmxWrXZWxczIzyEuXHFt/SE/
/4USxN72ZKjtnQAjHBDn1Rk45sOGDSuQEc/fBhoIUZauBNEY1eMDc4RQqfrv
kZUO2ct9boncabStCTFPCwyNKxPQsmTpaL8SYb5+pb19vPFGqOQsY+QKjaBF
7geWP/CQsGdemeA7BB67lh8Gz0ml8hxT8vNT/vHzk8TPTxQh2KaE2rMt+2Dw
s2PHjgIZ8XxvEGk7cmEgMi1LlhEqVL9Xvmp6VOVHkZWzIqsK5apkRVXOjKzy
ODI6I7LKrYiKv9jKfxcW/kGodUuQ6Q3/0BGl/TuXKPNiseKRvsVCvX3pBKIH
4UqBlgeiVcTLwZpy1Seh0jetdOBNUzjEzPypXlp+jnPwnODSriNPjR8sJJKy
QLDF6lvUSdnHSzrV9MKFCwUy3Pne+vfv74gf8BfgmL63lXsYVeVmOLngrWiR
0anhlUSzVbhnr5Buj35sq5hlrfDEUuGJtcJja3mwNEs5csWAEOvnQeb9wWFr
/EOmlA6MK1m2afGSVf2K2X38/L19fDDE8pAAc2C+Xl4zywTh6Tlns+PnBEVI
lXkd1gQ/yM+8PNd/fpT4OR1qW+vgwlCK3wJd4lUgY/00WlJSkpMQGlzSqLLB
QlRlvOAtXjaZ2U1bBWLWKGJmtaWao9JMkQ/CIh6GRT4Oi3oYVu6huRz0H4VF
wv7fjPbjBut3wdbPgswfB4VtCzAm+Yck+4cmUWOdBP+Q7QGGH4Kt14ny2PES
TKrrJHCey8ZOOT/uOG1ndirE7ML1D7X8YCEafiztHa+T5/np169fgYz102hf
ffWVm5MrOHl6BvoUvRQefS+SXogyQsTmlr0iGMHGVv6mtTwBxsJRZIpQ2Q1T
xHVq14zhV43hsP3DSPanmiJumwCnqDumSGa3qaVK9gc5pUu8vAZL1R1EPvKp
Xs75wSz+pKv8HAg1H5Y8F/JzNMT6dYiltJePo5O8sGHws3HjxgIZ66fR7t69
i1fW1f++NGpNCDEJ5avcpMwQbJjmIDAWbhsWKW4lcv6g2Kj4AbtiDL9M7ZIx
HLQI7aLUuSDZeWM4uzbLGYP9F8f8nFSWfbT8HFLyA+ay/vxL4ochdCbUvqBM
oFt20+JYczt79myBjPVTanj1e4d66+lew6/4vfDoVJEcKjgIj0XpsxAb2Er8
/CFhg3YVTAkPGgKD24scP3htn3OGHIkPf41TVealjZwx4867/2L8nDTY6vll
M2fhRZ1XeHj4c7a+fciQIU748aAh7seh1ke2iqKrQrWxKMlRas4fEjzXqOZc
l8hBeK5IysPsoqQ/F6Qtu7APBjxYXmYFQ9Uiw5Nc2KO72ueQEh683cDJPM+f
osH/+GGgyZOeSZ0tPzExMQUyyk+v4Z2UnUxkwM+qW8nSgrWCNkhWkcPzI/ss
jezw5EBsA4YdROhXSg67KhTGzBgwOyoYHleu8+FrPirxYbXig1R/XOPnX+SS
4DI/KaH20aX8sxUfDH6WL19eIKP89NrBgwedhNBeNJEv6uV9whR+31JOxkYv
VEZsbkjwXKOhMq85jB+GDYt8mJ2X+GGXpDsrgaRYpGGQxYdVe45TeNg6riN6
4vOTxI8L8bPZYq3Mrf+hmRf5X8oXzabsw/jJy3Va/pwtPT3dSQgtSpCH+7Qy
wYK1oiw4XJz8hybUEQMeTbTDNIfFPExzINrBsAevJ5YiFplZwcfq6MKYzG2x
RYZHsot8fnRVf8xUf74xWI+GWP4bYiZvEmrdFmDIds7CC29oHhLyXF6TuVGj
RtlNpHpafYv+ERYB+bWoNhQe3lWhn2LkXNMLlRk8v9OYhyVcCA+Lefi50TNU
iPiwR+m8ZHiO64XNWufFisauxc+VLNavAGm6yPD7EOvZUHvvEmWydV7IT7Nm
zQpkfJ92GzlypHN+MJHfERD6JCxKFedcV8Y51ziEVDHP71yq/juXql/kEvZz
HDxS2i5GztqwRzVboZot1XVebMbqJ5f8F4t/TtEzvOA//TY4LMjXJ1vnhfzM
mjWrIIb3qbdt27ZluxYIfmKNipV4GBZ5S89bXeMyLN4ua/hhtFzUBMy/csyc
Ufa1ysOqhcdzBk8+8oP5F/yn8AWXlQ2GX1aOZvHc3D7//PMCGd+n3fCURudn
hbhTL/afYEtGWLmcwKNxW+F8hs5rjjJatup6Lk3OLpeatad36SrPYem2O2ze
IY/8wPucN9qa52DOAuEpXry4a9f5+fO3hw8fBgUFOXdhKEHxJf2zzFHMSakK
O5c12PBu66JSdrKFJ1vl0T29AvnRKg8vPgddzb94fuA/+iTI5OPl7eyujRw/
tWvXLpDBfTatefPm2fIDiXxpb58Uox2i6OtKzXEOz+9SwKzl5zy5m5tdZbr8
6CqPo9NzdAuGzHPlCz9nQu0TSzu7to+KHxfOFvwLtfHjx2fLjxeNoheUCXlk
imRO6qoDcn6TKjwXuDxLQQ533wFaJNSRIG3MfJLeyUt3bTx/bo7WDirFJ4/8
HKX6UzEHZR/GjwtnC/6F2u7du3OynB6eUcnX74YJsIm47IAclqRfkjRHZaxC
eFYZHp/WeK4zDhKu43phM0vYefE5xEU+PDx55AfS9h0BhiI5KPt4SWvGnrNp
U1VLSUnJNoT2wkTe02NvoOm+KUoVHvOuik/Vedk5z81NnFXGxqf1ZIfnh/dZ
xxzAc0ijPyp+fswnfi6E2nrmrOyD4lOuXLnn+2I7EEKHhYXlyIV5urctXvJ+
WASLeX5XosIzo5iYkO6VI91uQCwv655JoVKeE1yR8Bh3pVzdE3MYObzbUomP
y/zg/eO+DzIHeOeo7IP8dOnSpUCG9Vm2Vq1a5YQfXLT8faj1lilCiwrGPKpV
PUDOeTpDwd9oSRUtn1ZOT5zWxMw/c9Ojx7g7mTqCh8XMWuXJIz8/GOxLHN+J
SZefNWvWFMiYPsv22muv5YQfLypB40oHpJuifleGxBdEhMLZ9AT6LCSHKY/E
jOKmJzw2SI40Q2pjeZaq2uycn0PKU0QP5h8/3xltDf3072GqbXhS5Pfff18g
Y/os2z/+8Y8cnpEKTwrx8T1vtF0zRmj91AVNbZC/xRtbknGGi5+1a8O0953k
yTmmPJ9du7ZZxY+uucZPbYttU6DJyzNn9OAdyYOCHN1V+XlqFy9ezOF1q3A6
bLV/yF26El5lWn7OScvA2DIMVaqOAc/pUHLpA+2qQszZtdk6g0fLDzsz4kfH
FLnGTz1reLdSZZyfYarip0kT9Xs+l+3Ro0cRERE5d2Ev+BW/aYq4pNQc8FY8
Odo7A2qlRqs52oRL5bMczXAdUq7QcBT5uMyP1WKtZrEF+hYtkuMzbp/jaVNt
a9euXQ75ccd1rUGmVFMkv9ydZVhsAQ9bA8YvgOej5TOaIuEpZZGZiY8qZlaX
eqRS86EciI9r/ERYbTazxcfHJ4fXncA1Y3+Te0dCe+ONN3LIjxeVoN4lypD7
kEonSoDpTmbxJ22dViqPCpuTyllR3et+6wfMuLZQyrmeHj92s8U3x/y40duj
uHCpjb9oO3DgQC748fIs7u39U6jld1lwxJmIs5o1YNoijyPZOe4AnmyzdX6G
PSf2bPhx7Tpjf9GW7T2S1MfHw3166aBUYwS3VtmqNS08pzRxMj2BS5yeUIU9
P3MFn8NKfg5JFyFk/GhlR6tIP7q6/tAFfoYPH14gQ1kgLSsrC++gnVN+PD3D
i/pdNNguKm/CflZZITyrKRIyfviV8Nw9i9U5+8/K09iRH3bXG3nyQpl/8aeI
6vKT2/XPueIHg5/ne9pU27p27ZpzfvAyL5sDjDckCaJmVVULtXfWPq0sFfJn
cvE1w+Oa5Oswh8oR3YhakqYfldGRNsF34fpjueIHi2lnzpwpkHEsqLZs2bKc
8+MlrWu9YRKX8bC0nedHe8UM/irfKuPh4aMgVcGQkXNYuh+lKin7kfNrupbD
+zcNGzwEmHGNn4iIiAIZxAJsX3zxRa6uiwiJvLun5xch5ivGCL7m40h/Tmum
t7T510npGizHNfwwio4pC9H8dVpwFv6IU3iQnwUafpo3VZ8i8erESYwfaja/
okVzyM/f8PbZly5dgpQztxI0tJR/Gi3+sPxdqz9aL6Z3Pg7RHz6cdjT59bNe
gMR7tKPKPVo7F2qZrOTHagrr3rWb6oAsWriQ5yfSZi9ZokS2/GDwk5ycXCCD
WLBNe8nlbPjx8gz09j1psP7O1X9UppvRa88HxD47pZ0/yYKPiI7rwZNb+zXU
0ivMFsLzYzSNHjVKdTT27d1nCzPz/AT4+2c7y4OX2jh27FiBjGDBNud3ytZH
yMN9UZmgO9SFMWZ0JeisZubrF82cO0vEVAueVUQdV/JzLDdGX2upY7aFcfxY
jKaVmpuHQgAMXPEhtNloyn6hppubwWB4zi61kcOWkJCQa348Pav5FbtstF+g
8Q9SlMKZahaeIaR7PYSTEjZI1EmptKi7fv64Y4/mxMB57TdYTRarXRH/mCH8
0x6QKhUrcfEPQaiYn182p8v9PdaM6bb//Oc/ub20OF3X6rk/0PQHJ0H8iYHa
VRy651kwF/aLssaIeT27TpSjyY4cGiD3e6h5rPLizxDkRNnsuqdoTRg3jg+B
gJ+QwCB3py7subzURg7b1atXHV3X19kR83TvWqJkGp0OQ1qwo10574QiR1Nj
J5T8kD8Z1KcQ5txAfL4zWCuYyfUQ+OAnplt33QPy3bffWjgXhgj5OZYgl2+s
/Ny0WrVq5ZYfepkXr4Ohlus0EcNLIvw5+bkSah5vsgVyPGDws3fPXt2jAWFM
/Tp1+CdHQhRkMDq6Nw0GP48fP37Go/bnafHx8bnlx0u6CfK9sEggJH/5UVle
+Pkt1PyegSiPVZm5V6tcJTU11dEBeWffPngOjxA4u0D/AN3rJv2dgx9s69at
c4UfL0+LT9ELZAm9YkUQH/+wWFqFELtIlOrMHW12Dx38qwvwQM5+2GCpa7YZ
VOJjMK5audLJAQExeble/XDlqyCX9y9TRosQHLrExMRnNlh/wvbtt9/m5HQw
VcN1rRsCQu5Ii8ryix++z9Z+5Iqcnyk8J0LNLcPsQUoMQFhqVq128+ZN58fk
m2++UUdBFhspB5Upi/dZw4OAwc/x48efzUj9Odvt27ezvSiZvgR5ujcoVuJm
WMRvGn7YvIYTfhyVhrTnGJ42yJMdObFLpOZsaRVmVYU9yM+e3btzcljmzp6j
8mKoQqFBwd7e3piRwUGLiop6vs8WzEnTvXdbto3eWdLz06Cwm6Zw5/yoTuc5
qwmK+KWturVrLCc6CZPQzodar9JqT22zLUgDD0jK0EGDc1joAy/WtmUr5XSY
iJAtzFymVCkvOm0B0ePTHp0/fxsxYoQL/KAEDShZNi0snJw26Jgfdgr8Obqu
VcvPKaf8nBEr1QqZYg6OnuJhvWSwXjVYvjXaRoXZTRarQQ+ehvXrOwmbtQ3c
3Mv1G2gRgoweKII39PHydh5K/U3avn373OhNVN1z0zzcyT3CSnl6ng4xpxsj
bhvtqQYb2i3J2J7bRluq0XbDYP/DYP3DYOPtusGKdtVgu8o95O2awXo51HaN
23OD7LQAM1cMlpMG616jbViYPcpCfJZN67aMptrVa6SkpOT2yFy5fKVls+Za
R4YURVislcqVb9akyZiRI1csW/bW9u17du36u9m+PXvemL+gRLFipUqWLFOq
dG6taMkSQ0JMW8MiksLCE012tGRTOFiS9JDsCQsHS+D2MFtDbVV2ttKoeAhv
tdBkmxRm62a21SBJliWQnrSlHWiAp36duqdOnnTtx/XgwYMB/fqpwmle1kID
gwJKlylTomRJv2J/TwssXRYEOcoe7pqFWK2lLJbSrlqZPBgwE2Kxhinntvh5
CkuoqUvHjnm/mhzIC6iQ1pepFelvaU6OyV/XyHCHmV+bPCW/bj77v//9r1Wz
5iA4zikqtL+6ATlgEPp+9tln+UIOa5C7ffCPf7Ro1gz/i0KQnieD0UTNqV+n
zs6dO5/q5d9PnTqVsGZN21atIZdHlgrtL23AT+OGLy9buvTgwYNPD5vCVtgK
W2ErbIWtsBW2wlbYClthK2yFrbAVtsJW2Arb37D9P2++Iw4=
"], {{0, 192}, {192,
0}}, {0, 255},
ColorFunction->RGBColor],
BoxForm`ImageTag["Byte", ColorSpace -> "RGB", Interleaving -> True],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSizeRaw->{192, 192},
PlotRange->{{0, 192}, {0, 192}}]\);Partition the image into color segments with a color distance of 1/8 or more.
colorDistance = 1/8;{colors, masks} =
Transpose@DominantColors[
MeanShiftFilter[img, 1, colorDistance, MaxIterations -> 12],
Automatic,
{"Color", "CoverageImage"},
ColorCoverage -> 0,
MinColorDistance -> colorDistance
]Remove segments that are too small or too thin.
cleanMasks = Map[Opening[#, 1] &, masks]validColors = Map[(ImageMeasurements[#, "Total"] > 0) &, cleanMasks]Extend the color segments into possible gaps using the grow-cut algorithm.
components =
GrowCutComponents[img, Pick[cleanMasks, validColors],
MaxIterations -> 5];Convert all color segments into binary masks.
completeMasks =
Reverse@Map[Image,
Differences@
Table[UnitStep[components - k], {k, Max[components] + 1, 1, -1}]]Convert the binary masks into BoundaryMeshRegion objects and extract their polygons as FilledCurve. Collect all FilledCurve objects and their corresponding colors into a Graphics expression.
MaskToFilledCurve[mask_Image?BinaryImageQ] :=
With[
{bm = ImageMesh[mask, Method -> "LinearSeparable"]},
GraphicsComplex[
MeshCoordinates[bm],
With[
{lines = MeshCells[bm, 1]},
FilledCurve[Split[lines, (#1[[1, -1]] === #2[[1, 1]]) &]]
]
]
]icon =
Graphics[
MapThread[
{#1, MaskToFilledCurve[Binarize[#2]]} &,
{Pick[colors, validColors], completeMasks}
]
]The resulting graphics icon is scalable and consumes less memory.
ByteCount[img]ByteCount[icon]