Mudança fracional cumulativa
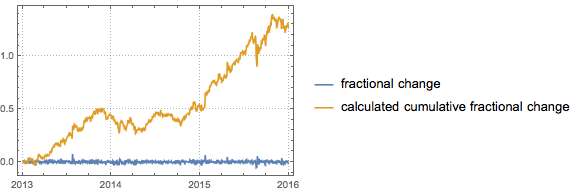
Calcule a mudança fracional cumulativa do preço das ações SBUX para o ano de 2015 da série temporal correspondente da mudança fracional dos preços das ações SBUX.
mostre o input completo da Wolfram Language
In[2]:=
ts = TemporalData[TimeSeries, {CompressedData["
1:eJw9Vwk0lV243oYifyIkSaWBUJlS8Zf2yZTUQWQOxxwajJnZ5nkeMhUVihAZ
kmifSsVfEaUiiaJoIkWi4b7ddddtrRbrHN/+9n7eZ9pr7U8YOXEihDjg/9e/
v9wJj1ycEoRR0eF9fJV+GOXuWGZwYQ9Ggl6u9S7WdCjg5/45tQyKlgQmcv22
pKRFJom/LByjiC1yXw0DKGIlKNj5H6VoxdMB5SQHis6FC30ucMboi22ewwFY
z824WP2dG2aMS26Ta42kSPEdz/tEFh7i2MPQ5i7FbA9y/2ZgEiU8wTfiGkIp
2j4x3ugXglHlEa63yXYYGZlw63EkYlTzevPH64kUre3cX+0D6/5i7T760oki
i8+i823uFCUcb7h2JQKTbrUAx0YPiu4GudVG2GGy/BY11A+jKLx550CCD2Wt
P352qX4ORT0DOprZLMyu4tI54pFNkYzqropsXYzK0l+5B6ZiQnbwX5WCc9cc
97uVbILZlRmtM//lYlRhfm83ty9G6Erb3tEdGCnZht+cS8HoiKK6dnsyRot2
6b6zi8bIQWWyoCgLI1LOjoyD85gnLlW/aUhRUsTMjIAfRZwreNI7YJ2kwjTB
rlSKxmwvbri2nRLrOvOGT/EUVe9IZ907/HefmoZF0Zj0JHAriwfBPjMKPGv9
MPkurlpaHEfR4vOtDzkDMbo4+vSwuCNFhu2+Mrx7MVoXos3NbUbRotXDmCcP
MziDrAMvA/6y60ZfiMN+BLwinvf5Ai6ynnuqTsL+KuNuc8N7nbOeMR4DH5Zk
JSueB9yflDZ7PQnH5JKC8Kb3pyiK0/eXlUvB5LOwr8veIEqa1i+puhxGSfyl
V+cl44BHjkfkez0wkgk1LFBKwGjrt99p5qGYHMqLlpuIweh5CPn2kQCu6Qcl
H0RiVMJedDDLEzP0+o0YabEUST9UyjL3wIx2U/FPWnkYFd+f3KgUhdHhYKWg
xSYUGakxBueOYpQlXVDH0KNIcGI1YcJ7o3y7JjZ7UaSbWC7RE4NJw6eYC9fD
MVs3eEqxCN7ncTpnrgb40Rh2SU7Wm6It0VHZXwG3zwNrZsIsKGrovTYmEUXR
VeV1nucAR562VdrLkzF7oewiERH4fJTrDSvPkZKdhf7v9gNu5f0JzFs+GLVi
64XtLEpK/vszyZFG0T2l0NemMZglf/CtnmsxZsSf1St9nobJYdv05axoijZP
X7pjnULZ9qwnftK5mGjxGq76cZIiCTq7rw/280tv09ypNMxICCnSE4imrJ3W
StYWGZRxIaY/pgTOYVhzXjoW1ukWH1e0isVsDsKQbkvDSF6E0ehgRdGJ3bfj
vJwp8dO+ogs4oOBf2RocoNf7Rc3PdcIw+jF/vTM1ABNvluHELvjc0DMoVwl0
q1ivIPliF0WPnDh3l2ZgJMo/GOsFvJD599yY8gE4741VX0/COeX5zN09Myn6
bc4j2g1zFizSvpnghVHoY75yB3c8pHFf2GZLFiX6E57G7amULNIUs5s/hRmz
vkZ+IXWY8dHcL9cFeHZ/4ey0UwhlD4QYDKpGUJTb8WfGpwijueEHpu9g3jL6
gwW14CtWcq2XLyRQdvubpKWy4RTNv8RTOqAvHWMPNy9biswtN5/bY40JPVad
vg90r9hV/1E7hjKYe0PLzoOumiL6BO7vpMg3TU/jkD9F+q8iLqWC7jxejikq
gE6WcSo07kzHyH+UzL81wKj5eYVpyCGKfk1W3iK5FIkKvd9kGQvfM7NfOLli
9vaXcpa/YL8TgZdsrFMx0r4Voz0SCr75pDHUA567gO2u7ANd8G/et3M0DrP7
eVVcZfMw6RTc5r4B5sQ3VNB/9Dic0zO2s8yEEuMixZnXnhR1mb7Ovgs6rxNp
3G6bjkmTvYX+N8DpQ3i1W9URSlbynj3rFUXZPsYSwZtgnfSxSJ0AZ4pqlx78
EQdznl0/8PiZLSb/LslKWAr8HvMTG1V1xIghsL0wUA0jXR+zX3OAj0hDR7l6
MEZ3J4+UZwbToe6j00pN6cDvo3oluscoaatvatQH3T2uPtCVEwG+YNxzPuAY
ZvgzRVMhB9iKYtcFbwJeQhdXXbOB7+/pZJaWgZ8k9cZ1/LQBXQpWVaRkYPKc
lmVFRVPGdLh0eHY8JaIenscyga/RJan8nKATYcEXyVWA65X54do1gCOyMJnf
74zZOsIqzfIw5//9V9zC4Hi0duZ8Fmb7Z+/eHwR66EQF8igf+O9XXZ5dgNGg
Y2+pAuSA40+nYEtzigqb8pxyAcc3PRvWLIfzzsYKpilpYUZ1ro2bE+indVcu
VxzkwZqvwuqZLhTNpZxhl5zCSERyi6CoPSU/jvPWShBKFr5Qbj8APCxxWMaU
MMWobqmLpADwv33lgHIh4LvkeXSLdiAlRxLeMa8kUHTRQ9LvEuRemvdq77/5
FyypvDHaiRKuwoWZ8mco8ulZMTMB8+R1ExGWOYhRfoP8zT7Qa8kLnel8M0yk
XD/t7PGm7PuS6IVTNiabadveKfD7nsS8YmHw48uGI9UuoNcyZQF5aTeMVhAt
WVnQn8mOb2/F4JxIvvdulSLg+vrOi8ssylavHCl8Bfx/8uBijaULJS4NYW63
wMeaI5YFzICvZxH19WzAKdLilHMG+E+c1JrvKUzM2PSzc3dXMfjAe/738aDr
Pc+V5roiMfvZqgxFJcgbdIKZv8OXMh64NL4VBd4Qmr8E61Ck3SHYZAvvmay0
tlfIweTx8s0yvNGUjM53J5R70mLRoyekpGBdE079y7zgm1ZWuZ1hMZSdqrHy
3jfA57jNo4TxQugLfILhyfYUfeIXMZIrwETQu1rjLsxn57hp1QLQ/aSFXsox
OO/S3RuXqP71Q7cBjtPwuZnhdrVSL8xYt77n2+ckyjhqliHxB3hk/m9m0xVX
jIQleZelJ/4frxBiHVj+pdq6kJIbx4MP9gOfLcc+uTlBrj4b0Yr2gnMNTgVc
0Q2m5L5j3HU90GPRGVua6UMJt+jXiJlMjEZpSq4r+MiW+dxCP5iPTM9IwUnI
+81mX86wCC7eq/7bCgPPDTZ37i+0g5zupUf7jaEfra8dV4T+Eq8bbjkP772Y
qsRxKAmjvdnugYVulOSqBhWIxVPGx4J9KZYwv9YOOmmTDD42ytWiCH6nHih9
odUD+sCeE73t4BsXPG/szQZe/Gx/KtcN+WcZsrFhDaFDxcHrTDKzqeTIBX9v
njTI523Sh+Kgp9Rb6N8sS8KsB3TDx09FlNh+FT/RDP0H4b3GupDzxm7Rgj3g
k6KfNH6rF2JGWrDSr0jwu9HfflTLGyMfZsC8H+S2qlWj9hDMt79uwUNr0EnS
5UmuGzBX2hbO7AqhaLh8bAOFOdW87ziYrAy+vKxIGIVgMrz7UO8UfE+mX91I
84JeEWvtzoRz9su90Hxqj9FVg6tb74MOxQLPDo5GYfJFIu7SknjwMcFZm2Pr
MPo4tmNFaBJFqzPtXlXBeQOfv/SfBv9gfPc9F2CEGTEW+ybuxVAkOZru+MQB
/PCeswbkOBHK4PpyjmDGoiVWTm9PYdLR93DkMuR47ESM35u/88k4OrcWcqQ+
XqhmCeD54/ShHCbw/7vKIoclMF/D/LTsL9qYWPMtVG4iGLWU/PxpAH4wX8dX
mAd+8pT3n/QZJ5jjj5e3/8D7zz48ObAdcPE/xR83ATyJu+ymiY7AOsLD15Xc
MUPgTknvWdDJt4721/Xkb2/ZGt1phcmK4eNcl8FXrQVjljHgp8o9TqdN+yia
aVufqQA9xZ7NL348BHjrXTcUA9+r7o3nWQb+UT3IzumA3jN3fa/WJvCnwFtD
3kutKBHKET69NRaT/uGqls/Qr0vV1yj8cKWILbVQqooB/Oy8VqviidF4Z+rO
03CeTFn2NrtMSgzsjgakQl8y2BdQbwY8m1MMz+uGfvvsgF5npw9mf0/v3v01
DbNluW7O3wb+nDMbd2iD92o1KWgehHxrqs9bzge9303deaAC5lss/jTKB3hU
neLRpAk8kOwKvuoJ94cJsY6qdYDzo8ltz5jgQw8n1mXuhz5XbRyWbQ8+lxaf
dItPm5JQTqWNsaGUvX/wjoMH4CXqcjCL4wQm3CsPnVgJOCyR/lg9B3N6/6Tc
cciIouTPu5jQL5B0UEHgcuhtum2LN+2Dv+uf3eY/Dv5iuPKNkp0VRhJhm6TX
mv2/LxAO1RQeW0/KHvTiFVKH/Wa7iri3AO/jWla8/A7zXHnQk/8Y5KT1Zxlp
DlgfkZaC1cbQf6oz4seBl/rLKuaDwXdYGeMNffA9r2prTg7wWkX4xUodd4wC
zX3EVYAPPg4Xyh3g3Kfv9tzsyKQMnT9nxtLhuRPJqo5PMjAraVeRvyH4x3Tr
YikuwH2XpX/lfRPoz0Gnb1Y5Ysb7rpYrS6Ev65Qfdky3o+xHtW6WnZmYHZal
tX82kjKkVzsrzYFvlHlIRFyHPjmTfuqGGvTG9tuGK/OVqKR8IJO9owjWX7bh
gUoYJirN5xO0fSjq1Cg+dOwYRgkeB17axmPycMbihzT0VxmJdZkloDfBmfk0
D5gLJ8Z9lvBTcvWT/YnQ85fwjG7Vg/tavnPL4VWw3xqf/hIJ6EHRswFvBqOw
5J6QE8IGcH/4tlm7Uxv6goR5QJYb6IgdmWBkBfP1aH7zShx8fFZR+N954GPh
1Ks2Xgc4751Yk2FDjAZev/6jZwH3gcronU8Z4DelrGpF0JPvec7VrscpSssx
em4N98CszfkfnWFffoIr1ZAPJhZUPuRYFials8KXI8G3DJrRWPwJShwrJXf8
A/nd/uSffGfwcwV/rCvjBTnJIaR5EPyvjc/8iv0hjMQ4hp+xYF+5YbYaJyGf
JvdU9CY6Y/JyS7dfN/BDJ5RVzABcMpy7tO9DX9aq8+4ussCSxhaFFjynKVvG
rOXa3hzKKAzd/hj0QnzV3hQOAc5KuoYGyqDHQrGgNqskWG/Vmbyz0OMGQ063
iLEoklettVODnta73KM2NggTtGf4PxPgkwznzlLQFel/nnDOG/TgkuPtcTqT
sj8EDCtVEMr2/Gr/fCv0twOlv1Ri0rCgSfzVDbcgd9cosqxzYH8aMzM6poB7
3HhE/38n4flaPuwIPm4pfa4nHOZYwhQY/Q19Vvf647vqBzBSt2uY0szAjGeS
RinfamB/4pHGGaCvR4/UcrwdMWkdufu0L5yyp/Vfeuqn4+LuuvK0QMjPi2LC
hTG+mHCk/9e+EXDXGUt+5AHzPFD1WK4e8Jwp+ydgN5xHsqnJM51FGdhjsfE2
6HNv98tyRYPfuIgaNPlCP+xYvNCECT3X4sK+I5Iwz8fStdw58LwYV++XKWuY
i1nL8lHgq6RLRVQs3N//Hd758JYpRQv8+FzZ4OO7nF9Kqrhiom5/tWcafPnJ
B/eP2+D8Qce/jv52oKRluHskEHrRAvl1BaIBmKEyLmLzLAXuI76X+raBX/Ry
SW/5DHO2yRoofg34ij8Y2PktG/j74nRClgEln2wUlC/Del5bTzNPwz44/xP9
45uKGboeGqWR0Aes1k+Vrge/5eZQ1tbQh/u2dPLIOj/M6rlV0R2UQ8mvHxZ1
EX/z0E4kJnMlJXRbiU8+4FXMU/LbIJEWSz3YFiaXAXi0ajTLQn7P7g84k2aK
iVfy9AYCftuVLiO9B/IxY71aVBXo6uXihkMToJ+fnHZJAsCff0LieUcgh90E
pYTXgz5GHvmiJvCje0nd51qht8pMX/kkDvP+uFXtrjDgVWgXnmKkRdmvhJR+
ip7CxX3pntEzF/FQ0p0ry2Xh3ic+HndgAvg7dttg1dt9mKQXX399Fvx/bFnn
lDHo3vTpm82CoL+b5yPXfkinjDaHk3tGIyl53aBqkAXrO4cOaD6HnqG11//b
Ij+KzkQXhrFgv36nV4bdhXnoF/0p4QHcUkZWOniC78ZPHaw7D/vrrhhaus0b
E0Yd/4KlkLf1Cj1xIv4Y2e/QPDzpgtnTqRNffeGekRq6zmE74DTdPJDoB+sm
bHTKvuoCPHp3+2so5NYFgbC8HZEUuS5+bjoM6wr/uGR2AtazGKi3L4zAbM25
OeW30NNZ+87VeMhixnCNi1RfDkaaA7EKYicoYtxvP9IHOa/7pNKfG/rhl8+H
tI9Bn+4aut47BPwcHu5qBL9Fee8f6jEAby0zm63/akCuKfj2XYW+HrVqz00e
eB/T2kfLB3Rd9mlucW8UZjua2toKZFF0wLS1xg18/gxd+k8x9CmJ8/y78wMx
4n5SsEAKPg8ujfi+ygQXb0xc4lSSQcmWqYQtB8Gna9408tYDb/hssYEK8PNR
rPkCNybwb5Vf2BrwmRrLVOUC4Ifki0X/OjEpmoyfDFoDf//IsJnHcCNFU0Wb
Nr+A+dheVOHugP41e1fs/vEETNb9yp6ShVyudJV/gABH7bVdL6IDMVFie4nm
wPO75xyvmUGeSvPnbbKHPDs3oqlfCrr9VLEm5yzkXHba0SNvoN+3XV3Lt2UP
JUbs4+vKINe4B/2/65lhxKs5ru+1B/rHYpE8IXi/YsUCKS7ohYfVmX7fwA9F
Gi0uxVtgsovJbPzjQcl5cwdWGfRWu4ROOXyJFu8ou31Y7SJFn2VStkam4KGa
pVrctysxO1lWtHf4HCYPaudVj/nRIQdbO/2JNMoQ2fyjuTSHSpY3dIw+K8bs
Rtw5swZyUfXDhel68NONI56uiemYYR/XsVgPeCtkGtd3Mh6zzWT2j3kDrmmt
Bo0O4E/ebS51KbC/OQ7Be4oBGAn+tlMf2Y7JAc0P1SfDKDl8pv6mKuiS+eD+
0Cjo23HoAntBHCZPddzfJ0OPsOxOcagIpOzxuk+38s5DbsVFJbOYlK02cUo1
G/g/LCZqIAC9zahmmA35w+Y/wvXtI/BqS+yski7kU5ya2Ic1kIcNLnIatYD3
wAe9Sk7wRfXEoo0LCSb2ge/uNARQVqEN13wn+MxD8TdVeqCL7bKdK/09MFsy
4s/6O3D/aNb5ZaQA9+anAqJGSX6UUTljckod+kK50I27ZXCPl4jPSe+BXDjM
kYtxLPTDtb+cJRPwUMU7u0Hdv3N8Y5NnYYTJIXeqme9LSQovh9ox0JGUQ9Ad
R7hvRffNk43AAyfjT9oOcH8S7dpyMhJ0gwMyav6B3GOv6G9y96FsRjB7e1AC
ZbTzePExIS+Fvkf/JwHnjf/D/S3JjjIsLOqurYd7sUzL+Mu4k5RMFS7eUQ58
GbcI9wiIxowm5qXwneDvt7JDbx+B/jn5ZjBVSIqSBLtmiQXgc6z8VTMW2yi6
5F7YtgD64LuFElOfCyg7zvKD3vtz4CPct4ozwBc3tZ2MGPTErPa8vNENcG/a
wJHDuSIWe2wQ0Z6cgRxlNbmEOEBvHCi6O+sCvSTm6jsrLZi/bX1Jhhz0P50P
m25+h/xwMVLdIgT7b2t2Xz4NPvPoqN/lUbj3KdoUC1+DfXgG5LVdsKNkb8KX
yflUuOe+Eo+6Azjw5z4RyE+g/wNF8pwH
"], {
TemporalData`DateSpecification[{2013, 1, 3}, {2015, 12, 31},
"BusinessDay", "DayRange"]}, 1, {"Continuous", 1}, {
"Discrete", 1}, 1, {
ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1},
HolidayCalendar -> {"UnitedStates", "NYSE"}}}, True, 314.1];A série temporal é amostrada regularmente nos dias úteis.
In[3]:=
ts["MinimumTimeIncrement"]Out[3]=
In[4]:=
RegularlySampledQ[ts]Out[4]=
A mudança fracional cumulativa é calculada usando a seguinte fórmula.
In[5]:=
fun := (Exp[Accumulate[Log[# + 1]]] - 1) &Aplique a fórmula de mudança fracional cumulativa a série temporal dos preços das ações.
In[6]:=
res = fun[ts];mostre o input completo da Wolfram Language
Out[7]=